数学几何模型风筝模型人工湖
昨天接到一起案子,报案者交代几何题目无从下手。那么今天我们就来真破几何难题案之风筝模型。昨天办案者私信我说,现在的几何题好难啊, 辅助线根本不知道怎么画,就算听了讲解,遇到新题还是无从下手。这种感觉你是不是也很熟悉?其实很多同学对几何感到无力,根本原因往往是没有抓住最基础的模型。 今天我们就从一个最基础的模型开始,把它一步步套进复杂的题型里,而这个起点就是封着模型。不过,在揭开封着模型的面纱之前,我们要先回想一下他的前身等高模型。 好了解等高模型的朋友请继续跟上。我们可以发现,风筝模型其实就是由几个等高模型组合成的一个大四边形,当我连接它的两条对角线,并标出四个区域, s、 s 二、 s 三、 s 四时等等。难道说 这里隐藏着一个规律, s 乘以 s 三等于 s 二乘以 s 四。推理时刻,这个规律从何而来?我们不妨用等高模型来推导一下。 s 和 s 二同在三角形 a、 b、 d 中,它们的高相等。所以面积比等于底边比 s 比 s 二等于 o, d 比 b o。 同样, s 四和 s 三同在三角形 c、 b、 d 中也有 s 四比 s 三等于 o、 d 比 b o。 咦,这两个比例的右边竟然完全相同!也就是说, s 一 比 s 二等于 s 四比 s 三。根据我们学过的比例性质,内向积等于外向积,于是 s 一 乘以 s 三等于 s 二乘以 s 四。原来如此! 不止如此,还有第二个关键点,三角形 a、 b、 d 与三角形 c、 b、 d 如果底边相同,那么面积比就等于高的比,也就是三角形 a、 b、 d 的 面积比,三角形 c、 b、 d 的 面积等于 a、 o 比 c、 o。 同理,你能否举一反三? 三角形 a、 b、 c 的 面积比,三角形 a、 d、 c 的 面积等于 o、 b 比 o、 d。 没错,这也是方程中常用的比例关系。实战演练,当方程走进中考题 来看,这道题正方形 a、 b、 c、 d 的 面积为一, f 是 c、 d 中点 e 是 b、 c 上的四等分点。求 a、 g 比 g、 f, 我 们一眼就能锁定四边形 a、 f、 d 正是一个风筝模型,接下来该用什么思路呢?等等, 既然 a、 g 和 g、 f 可以 看作三角形 a、 e、 d 和三角形 e、 f、 d 的 线段,那么 i、 d 比三角形 a、 d 的 面积比三角形 e、 f、 d 的 面积,思路一下子就清晰了。 三角形 a、 e、 d 的 面积正好是正方形面积的一半,正方形面积为一十,它就是二分之一。二、三角形 e、 f、 d 的 面积,它在三角形 e、 c、 d 中。而三角形 e、 c、 d 占正方形的四分之一的一半,也就是八分之一。 又因为 f 是 c、 d 中点,所以三角形 e、 f、 d 再占一半,即十六分之一。那么 x 比 g、 f 等于二分之一,比十六分之一就等于八比一。真相只有一个,答案是八比一!总结一下,遇到风筝模型,关键就是, 一、识别图形中的风筝结构。二、灵活运用对角面积乘积相等与底面对应比例两个关系。 三、将未知线段比转化为已知面积比。现在你明白了吗?下次再遇到复杂的几何题,不妨先默默问自己,这里会不会藏着风筝呢?最后留一道需要你自己画辅助线的题目,期待你的解答。
粉丝24获赞234
相关视频
 02:10查看AI文稿AI文稿
02:10查看AI文稿AI文稿好,大家好,我们看一下这道题。如图,母公园的外轮廓是四边形 a、 b、 c、 d。 被对角线 a、 c、 b、 d 分 成四部分,其中呢,三角形 b、 o、 c 的 面积是两平方千米, 三角形 c、 o、 d 的 面积是三平方千米,三角形 c、 三角形 a、 o、 b 的 面积是一平方千米。如果公园有大小为六点 九平方千米的陆地和一块人工湖组成,那么人工湖的面积是多少平方千米?我们看一下,这是一个是 公园,是一个是四边形,四边形呢,还告诉我们的当中,哎,三角形 b、 o、 c 的 三角形 c、 o、 b 以及三角形 a、 o、 b 的 面积,那我们要求出来 a、 o、 d 的 面积就可以了,因为 求出 a、 o、 d 之后,那四边形 a、 b、 c、 d 的 总面积就可以求出来,那我们拿出总面积的话,那再减去一个 六点九平方千米的陆地,那就是一个人工弧的面积。好,那我们把过程写一下,那我们根据方格模型,那三角形 b、 o、 c 的 面积乘上三角形 a、 o、 d 的 面积,就等于三角形 a、 o、 b 的 面积,再乘个三角形 c、 o、 d 的 面积, 三角形 a、 o、 b 的 面积和三角形 c、 o、 d 的 面积已经告诉我们了,所以说 a、 o、 d 的 面积我们就能求出来,它就等于二分之三,也就是一点五平方千米。好,那么这样的话,四边形的总面积我们就能求出来了吧, 那四边形的总面积呢,就等于这四个三角形的面积和,那么就等于二加三加一,加上一点五,就等于七点五平方千米,那人工湖的面积,人工湖的面积就等于这个总面积七点五,再减去这个 陆地面积六点九平方千米,所以说他就等于七点五,减去六点九,等于六零点六平方千米。好,这道题的答案呢?就是零点六平方千米。
11汤姆克鲁斯 02:28查看AI文稿AI文稿
02:28查看AI文稿AI文稿九岁精通奥数第一集风筝模型这是一个四边形,连接它的两条对角线就可以得到四个三角形,依然需要发挥你的想象力,看像不像风筝,所以就叫风筝模型。 风筝模型主要研究的是这四个三角形面积的关系,把它们分别记成 s 一、 s 二、 s 三和 s 四,那这四个面积有什么关系呢?咱们先来看上面两个三角形, 它俩是等高三角形,所以面积之比就等于底边的比,也就是 s 一 比 s 二等于 bo, 比 o d。 再看下面两个三角形,也是等高的,所以面积比也等于底边的比,也就是 s 三比 s 四就等于 bo 比 o d。 擦亮你的双眼,仔细观察一下,这俩都等于 b o 比 o d, 那 它俩也是相等的,也就是说, s 一 比 s 二就等于 s 三比 s 四,这就是四边形中这四个面积的比例关系,也是风筝模型的重要结论。 进一步地利用交叉相乘,咱们还可以得到, s 一 乘 s 四就等于 s 二乘 s 三。 在图上来看的话,就是这两个对折的面积相乘,就等于这两个对折的面积相乘。比如 s 一 是六, s 二是十, s 三是九,那 s 四等于多少呢?刚才说了,六乘 s 四就等于十乘九,算一下 s 四就等于十五。搞定 刚才这个结论说的是这四个小三角形的面积关系,那大三角形和大三角形之间有没有关系呢?当然有, 这俩面积的比就等于 b o 比 o d, 由此我们可以得到, b o 比 o d 就 等于六比十,也就是三比五。 再看左边的大三角形,总面积是六加九,得十五,而右边的大三角形总面积是十加十五得二十五,所以左边三角形 a、 d、 c 的 面积就等于十五比二,十五也等于三比五,所以这俩是相等的。 也就是说,左边儿三角形的面积比上,右边儿三角形的面积也等于 b、 o 比 o、 d。 类似的,上方三角形的面积比上下方三角形的面积就等于 a、 o 比 o、 c。 好 了,以上就是方正模型的两个结论,现在问题来了,在这个图里有三块儿面积一致,那剩下这块儿面积是多少呢?
134A博士云课堂 02:28查看AI文稿AI文稿
02:28查看AI文稿AI文稿今天我们要讲的数学几何模型是方正模型,之前咱已经学过了。长方形中的面积关系,实际上,在一般四边形中,也有一种特殊的面积关系。例如在这个四边形里,两条对角线把它切成四个小三角形。 假设这四个小三角形分别是等高三角形,所以 b、 o 比 o、 d 是 它们的面积比 s 一 比 s 二。 而下面这俩三角形也是等高三角形,所以 b、 o 比 o、 d 也是它俩的面积比 s 三比 s 四。哎,左边这俩相等,那右边这俩当然也相等了,于是 s 一 比 s 二就等于 s 三比 s 四, 这就是一般四边形中的比例关系。有了这个关系,只要能知道图中三个三角形的面积,就可以求出最后一个三角形的面积了。 比如在这个图里,已知其中三个的面积分别是八、六十二,那根据这个结论,就有八比六等于十二比 s 四。接下来要求它,那就得用到交叉相乘了,也就是八乘 s 四等于六,乘十二等于七十二, 因此 s 四就等于七十二,除以八算一算等于九。这个图形一般被称为方正模型, 不信你看,很常见的一种方程吧。在方程模型里,除了刚才这个结论之外,还有一个结论也很重要。回到图里, b、 o 比 o、 d 等于上面两个三角形的面积比八比六,也就是四比三, 而左边俩三角形的面积之合是二十,右边俩三角形的面积之合是十五。不难发现,二十比十五也等于四比三, 这说明 b、 o 比 o、 d 就 等于左右两个三角形的面积比。有了这个结论,就可以在方程里把面积比转换为线段比了。 举个例子来说,如果告诉你 abc 的 面积是七十, a、 d、 c 的 面积是五十,而 o、 d 的 长为十,问你 b、 o 有 多长? 那根据这个结论就有两线段的长度比等于两三角形的面积比,也就是 bo 比十就等于七十比,五十算一算 bo 就 得十四。 ok, 来总结一下 方正模型里有两个重要结论,第一个结论就是 s 一 比 s 二等于 s, 三比 s 四。第二个结论就是 bo 比 o、 d 等于左右两三角形的面积比。
 02:41查看AI文稿AI文稿
02:41查看AI文稿AI文稿小学奥数动画第一集风筝模型风筝模型这是一个四边形,连接他的两条对角线就可以得到四个三角形,依然需要发挥你的想象力,看像不像风筝,所以就叫风筝模型。 风筝模型主要研究的是这四个三角形面积的关系,把它们分别记成 s 一、 s 二、 s 三和 s 四,那这四个面积有什么关系呢?咱们先来看上面两个三角形, 它俩是等高三角形,所以面积之比就等于底边的比,也就是 s 一 比 s 二等于 b o 比 o d。 再看下面两个三角形,也是等高的,所以面积比也等于底边的比,也就是 s 三比 s 四就等于 b o 比 o d。 擦亮你的双眼,仔细观察一下,这俩都等于 b o 比 o d, 那 它俩也是相等的, 也就是说, s 一 比 s 二就等于 s 三比 s 四,这就是四边形中这四个面积的比例关系,也是风筝模型的重要结论。进一步的利用交叉相乘,咱们还可以得到, s 一 乘 s 四就等于 s 二乘 s 三。 在图上来看的话,就是这两个对着的面积相乘,就等于这两个对着的面积相乘。比如 s 一 是六, s 二是十, s 三是九,那 s 四等于多少呢? 刚才说了,六乘 s 四就等于十乘九,算一下 s 四就等于十五。搞定, 刚才这个结论说的是这四个小三角形的面积关系,那大三角形和大三角形之间有没有关系呢?当然有, 这俩面积的比就等于 b o 比 o d, 由此我们可以得到, b o 比 o d 就 等于六比十,也就是三比五。再看左边的大三角形,总面积是十加十五得二十五, 所以左边三角形 a、 b、 c 的 面积比上右边三角形 a、 d、 c 的 面积就等于十五,比二十五,也等于三比五,所以这俩是相等的。 也就是说,左边三角形的面积比上右边三角形的面积也等于 bo 比 o、 d。 类似的,上方三角形的面积比上下方三角形的面积就等于 a、 o 比 o、 c。 好 了,以上就是方正模型的两个结论,现在问题来了,在这个图里有三块面积一致,那剩下这块面积是多少呢?
 08:08查看AI文稿AI文稿
08:08查看AI文稿AI文稿大家好,今天我们继续学习五大模型,今天呢我们学风筝模型,下面我们看一下风筝模型是什么? 如图,四边形 a, b, c, d 对 角线 a, c, b, d 交于 e, 把这个四边形呢分成了四部分,我们用 s 一、 s 二、 s 三、 s 四表示这个四个部分的面积,我们得到了结论, s 一 比上 s 二等于 s, 四比上 s 三等于 s 一 加上 s, 四比上 s 二加上 s 三等于 d, e 比上 b e, 我 们看前面 s 一 比上 s 二,我们前面学到等高乘以 s 一 比上 s 二就等于 d 一 比上 b e, s 四比上 s 三也是 d 一 比上 b, 那 么 s 一 加上 s, 四比上 s 二加上 s 三也等于 d 一 比上 b 一, 这是怎么回事?我们推导一下, 我们两边同乘以 s 二,就得到 s 一 等于 s 二乘以 b 一 比上 b 一, 这个 s 四两边同乘以 s 三, s 四就等于 d e 比上 b, e 乘以 s 三,那我们把 s 一 加上 s 四,我们看等于什么呀?对, 就等于 s 二乘以 d e 比上 b e 加上 s 三乘以 d e 比上 b e。 把 d e 和 b e 提取共音式, 就等于括号 d e 乘以 b e 乘以括号 s 二加上 s 三,在两边同除以 s 二加上 s 三, 我们就得到了 s 一 加上 s 四比上 s 二加上 s 三等于 d, e 比上 b e。 啊,同理可以证明啊, s 一 比上 s 四等于 s 二比上 s 三等于 a, e 比上 ec。 上面这两个部分相加,比上下两个部分相加,也等于 a e 比上 ec, 同理可以证明。通过这个一式,我们还可以得到一个结论,就是对角这两个三角形的面积,它们相乘积是相等的,我们看 s 一 比乘以 s 三等于 s 二乘以 s 四, 这就是我们方程的结论。下面我们看方程的,我们在实际解析中是怎么应用的? 我们看这个例题,正方形 a、 b a 一 b 一 c 一 d, 它的面积是一, 这和 k 是 这两条边的中点,我们要求这两条线分割的四个图形的面积分别是多少。那我们看根据已知条件,我们能知道哪些个图形的面积。 我们三角形 a 一 这 d 一 的面积是知道的,因为它是中点,看一下它是正方形一半的一半。三角形 a 一 b 一 k 的 面积我们也是能够知道的。 我们看我们知道这两个条件能求出这个四个图形的面积吗?如果求不出来呢?我们就想办法要加辅助线。 你看如果我们连接 j、 k 和 k、 d 一, 我们会得到什么图形呢?对,得到了一个四边形和三角形, 我们看这个三角形的面积还是可以求出来的。这个四边形我们看它像什么呀?像我们刚学过的风筝模型, 我们风筝模型得的结论是,这个面积比等于它这个线段的比。 那三角形 a、 e、 j、 k 的 面积我们能求出来吗?这是中点, 那三角形 a 一 j、 k 就是 三角形 a 一 b 一 k 的 一半,那三角形 a 一、 k、 d 一 的面积我们同样可以求到,它是这个正方形的一半。我们先把式则列出来, 得到了这个三角形的面积和这个 a 一、 k、 d 一 的面积。那我们还能得出什么结论呢? 这两个三角形的面积比就等于线段 j、 l 比上 l、 d 一, 让我们看一下它得多少,就是 j、 l 比上 l、 d 一, 它是一比四, 那我们看我们知道这个大三角形 a、 a 一 这 d 一 的面积,又知道这个线段底边那个比,那这个小三角形和这个 a 一、 l、 d 一 的面积比是一比四,那这个小三角形的面积是不是可以求出来? 对,我们把数字看一下,它们的面积是一比四,那小三角形就占这个 a 一、 g、 d 一 的五分之一,那我们就可以求出这个小三角形 a 一、 g、 l 的 面积。 我们知道这个小三角形的面积,又知道这个大三角形的面积就是 a 一、 l、 d、 e 的 面积, 你也可以用它占它的五分之四,直接求出来 a、 e、 l、 d、 e 的 面积。把十字列出来,我们看上面这两个三角形的面积我们求出来了,那下面这两个四边形的面积我们是不是就好办了? 这个 a 一、 b 一 k 的 面积我们是知道的,是可以求出来的,它减去这个小三角形就等于四边形 j、 l、 k、 b 一 的面积, 这个式子给它求出来,那我们看这个四边形 l、 k、 c、 e、 d、 e 的 面积,就等于这个梯形的面积,减去这个三角形 a、 e、 l、 d、 e 的 面积,或者是正方形的面积,减去刚才我们求出这三个部分的面, 这两种方法都可以求出来,我们就可以列式子给它计算出来。好了,我们通过用方正模型就解决了这个问题。我们第一步呢是先根据已知条件,看看哪些图形的面积可以求出来, 如果达不到我们的目的呢?我们就要加辅助线,把这个未知的图形变成我们熟悉的图形,三角形还有四边形,这个四边形是一个风筝模型,我们就用风筝模型,我们学到了知识,解决了这个问题。 上面呢?这是一个公众号,这个公众号里有风筝模型的习题,有兴趣的同学可以做一下。 这是我的课程内容,包含了 bc 的 大部分的知识点。呃,同学们可以系统的学习。
0登高远眺 02:21查看AI文稿AI文稿
02:21查看AI文稿AI文稿五年级奥数动画风筝模型风筝模型,这是一个四边形,连接他的两条对角线就可以得到四个三角形,依然需要发挥你的想象力,看像不像风筝,所以就叫风筝模型。 风筝模型主要研究的是这四个三角形面积的关系,把它们分别记成 s 一、 s 二、 s 三和 s 四,那这四个面积有什么关系呢? 咱们先来看上面两个三角形,它俩是等高三角形,所以面积之比就等于底边的比,也就是 s 一 比 s 二等于 b o 比 o d。 再看下面两个三角形,也是等高的,所以面积比也等于底边的比,也就是 s 三比 s 四就等于 b o 比 o d。 擦亮你的双眼,仔细观察一下,这俩都等于 b o 比 o d, 那 它俩也是相等的,也就是说, s 一 比 s 二就等于 s 三比 s 四,这就是四边形中这四个面积的比例关系,也是方程的重要结论。 进一步呢,利用交叉相乘,咱们还可以得到 s 一 乘 s 四就等于 s 二乘 s 三。 在图上来看的话,就是这两个对着的面积相乘,就等于这两个对着的面积相乘。比如 s 一 是六, s 二是十, s 三是九,那 s 四等于多少呢?刚才说了,六乘 s 四就等于十乘九,算一下 s 四就等于十五。搞定, 刚才这个结论说的是这四个小三角形的面积关系,那大三角形和大三角形之间有没有关系呢?当然有, 这俩面积的比就等于 b o 比 o d, 由此我们可以得到, b o 比 o d 就 等于六比十,也就是三比五。 再看左边的大三角形,总面积是六加九,得十五,而右边的大三角形总面积是十加十五,得二十五,所以左边三角形 a、 d、 c 的 面积就等于十五比二十五,也等于三比五,所以这俩是相等的。 也就是说,左边三角形的面积比上右边三角形的面积也等于 b、 o 比 o、 d。 类似的,上方三角形的面积比上下方三角形的面积就等于 a、 o 比 oc。 好 了,以上就是方程模型的两个结论。
26暖老师趣味动画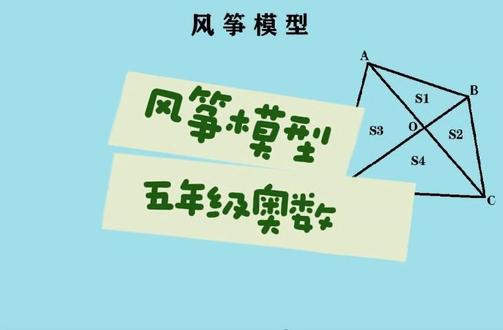 01:04查看AI文稿AI文稿
01:04查看AI文稿AI文稿这个视频我们学习风筝模型的特点,风筝模型是存在任意四边形中的面积比例关系。看图, 四边形 a、 b、 c、 d 被分成了四部分,面积分别设为 s 一、 s 二、 s 三、 s 四。根据等高模型的特点,三角形的高相等时,面积比等于对应底边的比。我们可以看到, s 一 比上 s 二就等于它们对应的底边 a、 o 比上 oc, s 三比上 s 四也是对应底边 a、 o 比上 o、 c。 这样我们就得出 s 一 比上 s 二就等于 s 三比上 s 四。 同理, s 一 比 s 三等于 bo 比 o d, s 二比 s 等于 bo 比 o、 d, 他 们就可以得出 s 一 比 s 三就等于 s 二比 s。 再看三角形 abc 和三角形 a、 d、 c, 它们的底边都是 a、 c, 所以 它们的面积比就是它们高的比,所以就得出 s 一 加 s 二比上 s 三加 s 四就等于 bo 比 o、 d。 同理, s 一 加 s 三比上 s 二加 s 四就等于 a、 o 比 o、 c。 这些风筝模型的特点一定要记牢。
32果宝特工 03:22
03:22
猜你喜欢
最新视频
- 2.4万大萌芽







