#你怎么看动画勾股定理
粉丝3906获赞27.6万
相关视频
 00:29查看AI文稿AI文稿
00:29查看AI文稿AI文稿养了一只小猪,并取名为佩奇,两年半后,佩奇长大了,男子手里拿着庆祝佩奇长大的见面礼,兴高采烈的向佩奇走了过去。佩奇看见直接沸腾起来了,直接一个劲冲出了栅栏外面。男子见状立马追了出去,却发现佩奇已经掉进了废弃的池塘里,他琢磨着怎么把佩奇给弄上来,于 是。啊啊啊!
 00:21
00:21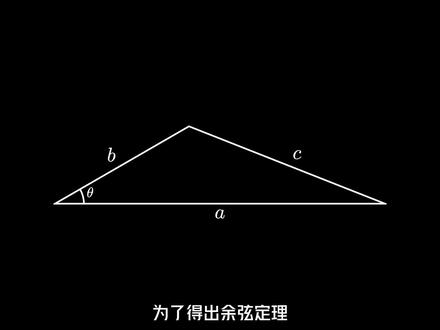 02:19查看AI文稿AI文稿
02:19查看AI文稿AI文稿假设我们有一个三角形,他的三边分别为 ab 和 c, 我们称对边 c 所对应的角度为非他余弦定理给出了这四个直之间的关系。为了得出余弦定理,我们从三角形的顶点向底部下垂线得到了两个直角三角形。 黄色三角形的斜边为 b, 这意味着该黄色三角形的高度为 b 乘以菲泰的正弦值,而底边为 b 乘以菲泰的余弦值。因此,蓝色直角三角形的底边长度为 a, 减去 b 乘以菲泰的余弦值。有了直角三角形的图像后,我们可以在直角三角形的两条腿上画正方形,在斜边上画正方形, 这些正方形的面积为 b 乘以 fat 的正弦值的平方, a 减去 b 乘以 fat 的余弦值的平方和 c 的平方。根据勾股定理,我们知道 c 的平方等于 a 减去 b 乘以 fat 的余弦值的平方,再加上 b 乘以 fat 的正弦值的平方。通过代数规则、勾股定理和三角函数的横等式,我们可以得到 c 的平方等于 a 的平方,加 b 的平方减去两个 a 乘以 b 乘以非态的余弦值。这就是余弦定理,意味着我们已经用勾股定理证明了余弦定理。 我们还可以将 fat 等于拍二带入余弦定理中,证明了勾股定理和余弦定理的等价性。如果你想知道当角度 fat 为钝角时,图像是否仍然有效,那么我们可以得到一个三边长为 ab 和 c 对应角度为钝角 fatt 的三角形图。在这种情况下, 我们可以下垂线并绘制一条水平线,构建一个直角三角形。在这个蓝色直角三角形中,我们可以看到一个黄色直角三角形,其角度为拍飞探,因此它的高度为 b 乘以拍飞探的正弦值,底边为 b 乘以拍飞探的余弦值。 然而,我们知道, b 乘以拍飞泰的正弦值实际上等于 b 乘以飞泰的正弦值,而 b 乘以拍飞泰的余弦值为负担, b 乘以飞泰的余弦值。因此,所示的蓝色直角三角形的高度为 b 乘以飞泰的正弦值,底边长度为 a 减去 b 乘以飞泰的余弦值。最后, 我们可以再次应用勾股定理来得到同样的横等式,即 c 的平方等于 a 减去 b 乘以非太的余弦值的平方,再加上 b 乘以非太的正弦值的平方, 这意味着我们可以使用代数运算得出钝角情况下的余弦定理。总之,无论夹角是锐角还是钝角,余弦定理都是适用的。
5.2万派蒙科普 01:06
01:06 01:47查看AI文稿AI文稿
01:47查看AI文稿AI文稿勾股定理是初中数学的重要内容,今天给大家分享一组动态图片,让你的课件更加形象生动。神奇的勾股数用来做课程导入,激发学习兴趣。 注水法讲解勾股定理解释两个小正方形面积之和等于大正方形面积。 勾股定理的证明方法很多,赵爽利用弦图通过图形的切割和拼接进行证明,也是我国古代常用的出入相补法。 欧基里德在几何原本中用等级变形也进行了证明,还有传说中的必达哥拉斯拼图正法,再来看 看几个应用势力吧!我们可以借助勾股定理做出长围根号二根号三根号五等等的线段,形成无理数海螺图。 也可以用同样的方法,在竖轴上画出表示自然竖的算数平方根的点。 还有做题时常见的蚂蚁爬行问题,比如长方体圆柱体表面的最短路径,还有台阶上的的最短路径。使用这样的图片来动态演示,就更容易让学生理解啦! 以上图片直接插入 ppt 放映即可动态展示, 像这样的动态图片还有很多哟!你还想要哪些数学动图?快来评论区留言吧!
324小畅老师 00:42查看AI文稿AI文稿
00:42查看AI文稿AI文稿今天用赵爽贤图意图证明勾股定律。先画一个边长为 c 的 大正方形,四条边就是四个直角,三角形的斜边,直角边分别是 a 和 b, 中间留下的小正方形边长是 b 减 a, 大正方形边长是 c, 所以 面积是 c 平方。四个三角形面积加起来是二乘 a 乘 b, 中间小正方形边长是 b 减 a, 面积是 b 减 a 的 平方。整理就得到 a 平方加 b 平方等于 c 平方。 照爽玄图的关键就是面积拆分与拼合,结论是 a 平方加 b 平方等于 c 平方。点赞、收藏、关注,带你看更多经典几何证明!
26平方AI数学 01:38
01:38 05:05查看AI文稿AI文稿
05:05查看AI文稿AI文稿勾股定律的证明,这款金银双色大裤衩地板砖非常特别,你瞧瞧,里面真的有条大裤衩呢!在这条大裤衩里面隐藏着一个秘密, 直角三角形,两条直角边的平方和等于斜边的平方。用数学式子来表示,即在直角三角形 a、 b、 c 中, ab 为直角边, c 为斜边,则有 a 的 平方加 b 的 平方等于 c 的 平方。 古今中外,无数英雄好汉沉迷于对勾股定律的研究。经典方法一,赵爽玄图 中国籍牛人赵爽在勾股圆方图注里面画了这张闲图,用四个一模一样的红色直角三角形。这四个直角三角形的直角边都是 a 和 b, 斜边是 c, 依次相连,围成了一个边长为 c 的 组合。大正方形中间形成一个较小的正方形,边长为 b 减 a。 那么大正方形的面积即 c 的 平方就等于四个红色直角三角形的面积,即四倍的二分之 a, b 再加上中间黄色正方形的面积,即括号 b 减 a 的 平方, c 的 平方等于四。乘以二分之 ab, 加上括号 b 减 a 的 平方。整理一下, c 的 平方等于二 ab 加上 a 的 平方加 b 的 平方减二 ab 得到 c 的 平方等于 a 的 平方加 b 的 平方。不愧是流传了两千多年的经典正法,无需多说点赞。不过这四个红色直角三角形还有另一种摆法。仔细看看 经典正法二,变异弦图这四个边长为 a 加 b 的 组合大正方形 中间形成一个边长为 c 的 正方形,那么这个大正方形的面积就等于这四个直角三角形与中间这个正方形的面积之和, 也就是括号 a 加 b 的 平方等于四,乘以二分之 a、 b 加 c 的 平方。 整理一下,得到 a 的 平方加二 a、 b 加 b 的 平方等于二 a、 b 加 c 的 平方。等号两边同时减掉二 a、 b、 a 的 平方加 b 的 平方等于 c 的 平方。 哈哈,神奇吧,再次点赞!最后我们再看经典政法三、巧用梯形。据说这个方法是美国第二十任总统加菲尔德想出来的。首先画出直角三角形 a、 d、 e, 其中两直角边 a、 d 等于 a, a、 e 等于 b, 斜边 d、 e 等于 c。 继续做一个跟它全等的直角三角形 b、 e、 c, 其中两直角边 b、 e 等于 a, bc 等于 b, 斜边 e、 c 等于 c。 要求 a、 e、 b 三点共线点 e 在 ab 之间,且两个直角三角形在直线 ab 同侧 连接 dc, 就 形成了梯形 a、 b、 c、 d。 容易发现三角形 d、 e、 c、 d 是 等腰直角三角形。 那么梯形的面积呢?就等于这三个直角三角形的面积之合。好好算算,梯形 a、 b、 c、 d 的 面积等于二分之一,乘以括号上底加下底乘以高等于二分之一倍的 a 加 b 乘以 a 加 b。 而三角形 a、 d、 e、 三角形 b、 e、 c 以及三角形 d、 e、 c 的 面积的和等于二分之一 ab 加二分之一 ab 加二分之一 c 的 平方。 由此得出二分之一倍的 a 加 b 乘以 a 加 b 等于二分之一 ab 加二分之一 ab 加二分之一 c 的 平方。等号两边同时乘以二, 得到 a 的 平方加二, ab 加 b 的 平方等于 ab 加 c 的 平方。等号两边同时减掉二 ab, 就得到了 a 的 平方,加 b 的 平方等于 c 的 平方。
 01:41查看AI文稿AI文稿
01:41查看AI文稿AI文稿你可能没有听说过月牙定理, 以直角边为直径画半圆,以斜边为直径画半圆, 得到两个月牙 月牙面积之和正好等于三角形面积, 是不是很神奇? 总面积等于三角形,加半圆一加半圆二, 月牙等于总面积减去半圆三 替换 圈起来的等于零,所以月牙等于三角形 翻折便于观察。 分别三面积 带入提取八分之派, 根据勾股定理,圈起来的等于零,所以最终结果等于零。看懂了吗?
5.8万哈密瓜微课 03:31查看AI文稿AI文稿
03:31查看AI文稿AI文稿同学们,如果前面是红灯,你就会停下脚步。反过来,如果你停下脚步,那么前面是红灯吗?如果外面在下雨,出门要带伞。反过来,如果出门要带伞,那么外面在下雨吗? 如果物体在水里会下沉,它的密度比水高。反过来,如果物品的密度比水高,那么它会下沉吗?有的答案是肯定的,有的答案是否定的。那么接下来讨论的问题的答案是肯定的呢?还是否定的呢? 哈哈,还是先来看问题吧。如果直角三角形的两条直角边长分别为 ab, 斜边长为 c, 那 么 a 平方加 b 平方等于 c 平方。反过来,如果三角形的三边长 abc 满足 a 平方加 b 平方等于 c 平方,那么这个三角形是直角三角形吗?看完问题,大家有什么感想吗?花花老师觉得光凭空想是找不到答案的,不如我们画几个满足这个条件的三角形试试。 大家看下面的每组数分别是一个三角形的边长 a、 b、 c, 而且满足 a 平方加 b 平方等于 c 平方。现在我们分别以每组数为三边长画出三角形,看看他们是不是都是直角三角形。 首先,我们来看以第一组数三、四、五为三边长画出三角形。用量角器量一量,毫无疑问,这个三角形是直角三角形, 那以第二组数五十二十三为三边长画出的三角形呢?量一量,这个三角形也是直角三角形。 以第三组数八十五、十七为三边长画出三角形,会不会有什么意外呢?量一量就知道答案了,哈哈,这个三角形也是直角三角形哦。 接下来看看以第四组数七、二十四、二十五为三边长,画出三角形。量一量,果然不出所料,这个三角形确实也是直角三角形。 通过实践可以知道,如果三角形的三边长 abc 满足 a 平方加 b 平方等于 c 平方,那么这个三角形是直角三角形。同学们,像刚刚我们讲的三、四、五、五、十二、十三、 八十五、十七、七、二十四、二十五这几组数能够成为直角三角形。三条边长的三个正整数称为勾股数。 若 abc 是 一组勾股数,则 a、 k、 b、 k、 c、 k 是 正整数,也是一组勾股数。例如,三、四、五是一组勾股数,这组勾股数的两倍、三倍、四倍、十倍都是勾股数, 因为他们始终是满足 a 平方加 b 平方等于 c 平方的三个正整数。 讲了这么多,接下来归纳一下本节课程的知识点吧。一、如果三角形的三边长 abc 满足 a 平方加 b 平方等于 c 平方,那么这个三角形是直角三角形。 二、像三、四、五这样能够成为直角三角形的三条边长的三个正整数,称为勾股数。若 a、 b、 c 是 一组勾股数,则 a、 k、 b、 k、 c、 k 是 正整数,也是一组勾股数。观看完整版课程,关注花花老师!
3花花课堂![[动画演示]8种证明勾股定理的方法](https://p3-pc-sign.douyinpic.com/image-cut-tos-priv/09ed3b7eddd164a5ef437c1aa780e345~tplv-dy-resize-origshort-autoq-75:330.jpeg?lk3s=138a59ce&x-expires=2086988400&x-signature=1VICxos2T1lqVQuTVHn6f8kF2cU%3D&from=327834062&s=PackSourceEnum_AWEME_DETAIL&se=false&sc=cover&biz_tag=pcweb_cover&l=2026022107222956BE11296CEEDADB2FB7) 05:11
05:11
猜你喜欢
最新视频
- 22.6万地球百科君







