六年级几何图形燕尾模型
粉丝3.1万获赞6.9万
相关视频
 04:22查看AI文稿AI文稿
04:22查看AI文稿AI文稿啥叫燕尾模型?顾名思义,就像燕子尾巴一个图形,哎,这个燕子尾巴挺有特点,我们先画一个三角形,三角形的三个顶点,咱们都给他标上符号 a、 b、 c, 然后在这头边上咱们任意找一点,比如说在这随便找啊,给他标上符号 d, 零点一相连,也就是说这个 b、 d 把三角形 a、 b、 c 给他分成了两部分, 这两部分还不相等,那么咱们就把左边这个三角形,它的面积咱们设为 s 一,这个右边的三角形,咱们给它设为 s 二。哎,那我要说 s 一比上 s 二, 他就等于 ad 比上 dc, 那你该问了,哎,那老师你说不中啊,你得给证明 very good, 咱们到了六年级了,思维就得到这个高度,那好吧, 咱们就证明一下来看看啊,这个三角形 a、 b、 c 的面积是底乘高除以二,这咱们都知道,哎, 那咱们先把这个高给它画出来,给它设为 h, 那咱们先看一下 s 一,这个三角形,它的面积是底乘高,底是 ad 乘以高,现在咱们表示字母是 h, 然后除以二,那 s 二呢?它的面积等于 底乘以这个 h。 哎,那我现在让 s 一比上 s 二,你发现没有, 这个 h 除以二和这个 h 除以二,那就相互抵消了,所以 s 一比上 s 二,就等于 ad 比上 dc, 证明结束,这样没有毛病吧。好了, 现在啊,我们把这个都给他擦去。什么叫燕尾模型呢?就是在 bt 这条线段上任意的找出一点,哎,咱们给他设为 o, 看看这个图像不像燕子的尾巴。如果咱们就看这个图啊, s 一比上 s 三, 他就等于 bo 比上 od, 跟刚才讲的原理一样啊,然后咱们把这边给他盖住,看看这个三角形, s, 二比上 s, 四等于 bo 比上 od, 你发现 s s, 一比上 s, 三等于 bo 比上 ods, 二比上 s 四也等于 bo 比上 od, 这个记住了啊,说,那老师这个证明完了,那有啥用呢?哎,用处老大了,下面老师就给你讲解一个 小升初常考题,如图,各部分的面积分别是三平方厘米,四平方厘米,二平方厘米。哎, 让咱们求这地方是多少平方厘米?所以啊,刚才咱们证明这个啊, 燕尾模型是非常有用,解决这道题省老事了。那咱们看一看这个图,如何构建燕尾模型呢?哎,我们从这给他画一条辅助线,哎,这燕子的尾巴不就出来了吗?是吧? 哎哎哎哎,咱们把这一部分呢设为 x, 这呢给它设为 y, 那也就是四比上二,它就等于三加 x 比上 y。 还有一个咱们这么看啊,歪着头这么看, 这也是一个艳美啊。二加上 v 比上 x, 他就等于四比上三,把这两个式子 组合起来,这个呢,就是二元一次方程,是有点超纲了,通过解带二元一次方程啊,得出 x 等于四点二, y 等于三点六, 那么这个问号区域就是 x 加 y, 也就是四点二加上三点六,等于七点八平方厘米。虽然有点超纲了啊,但是关键不是让我们做出问号部分的面积,而是让我们知道 燕尾模型背后蕴含的数学道理。下个视频还是讲六年级的题,就是黑板这道难哭学霸的题,如何运用蝴蝶模型来秒杀?
253史阿婆画数学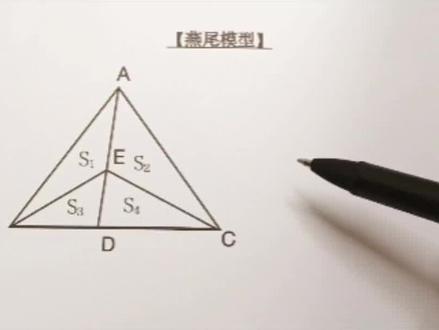 03:03查看AI文稿AI文稿
03:03查看AI文稿AI文稿燕尾模型是非常常用的数学结合模型,因为它很像燕子的尾巴,所以叫燕尾模型。这个模型带给我们的关系是,就是 s 一比上 s 二, 等于下面这两个三角形面积之比就是 s 三比上 s 四,同时也等于 b d 比上 d c。 那很多同学呢,不知道这个模型,也有的同学知道这个模型,也知道这个结论,但并不知道这个结论是怎么来的。那今天德祥老师就带着大家一起推导一下。首先我们看 s 一和 s 二 这两个三角形,他们是有公共的边,也就是 a e, 根据等高模型,有公共边的两个三角形,他们面积之比就等于以公共边为底边上高之比。那 se 如果以 a e 为底边的 高,就是要过点 b 来去做 a e 的垂线,那德强老师带着大家一起做一下。好做完了之后呢,我们这里给他标上是 h e, 那 s r 如果以 a e 为底边的话,高就是要过点 c 来去做 a e 的垂线。德强老师也给大家做一下, 好做完了之后呢,我们这里给它标上是 h 二,所以 s 一比上 s 二,就等于 h 一比上 h 二。好,我们再看 s 三和 s 四这两个三角形,它也有公共的边,也就是 e d。 根据等高模型,这两个三角形面积之比就等于以 e d 为底边上高之比,那 h 一既是 s 一的高,同时也是 s 三的高。 h 二既是 s 二的 高,也是 s 四的高,所以 s 三比上 s 四,就等于 h 一比上 h 二。那通过这两个关系式,我们推导出来, s 一比上 s 二,就等于 s 三比上 s 四。 所以英尾模型的第一个结论我们就推导出来了,那第二个结论我们怎么推导出来呢?我们再看 s 三和 s 四这两个三角形,他们不仅有公共的边 e、 d, 他们还有一条共同的高,也就是过点 e 来去做 b、 c 的垂线,德夏老师也带着大家做一下。 好做完了之后呢,我们这里给它标上 h 三。根据等高模型,两个有共同高的三角形,它们面积之比就等于高所在的底边之比。那 s 三如果以 h 三为高的话,底边就是 b d s 四,以 h 三为高的话,底边就是 d c, 所以 s 三比上 s 四,它同样等于 b d 比上 d、 c, 那我们第二个关系式就推导出来了,那我们综合一下,就是 s 一比上 s 二等于 s 三比上 s 四,就等于 bd 比上 dc, 你学会了吗?关注德祥老师,学习数学不迷路!
303德翔老师思维课堂 20:24查看AI文稿AI文稿
20:24查看AI文稿AI文稿hello, 大家好,欢迎来到明老师初中数学课堂,我们今天继续来学习初中数学几何模型,今天学习的内容是第九个模型,燕尾型。 本视频的题目来自万维初中数学几何模型,需要购买视频同款学习资料的同学,这里可以按下暂停键查看购买的方法。 好,咱们一起来看一下这个模型啊,哎,这个图形的形状有点类似那个燕尾哎,所以呢,叫做燕尾型,它的特点啊,它是一个凹四边形哎,可以叫做凹四边形 a, b, d, c。 这个凹四边形啊,跟我们平时所学习的那种凸四边形是有区别的啊,最大的区别就在于呢,他有一个内角是大于一百 八十度的,也就相当于啊,这个地方有一个明显的凹进去的这样一个角哎,所以他就叫做凹四边形。好,那对于这样的四边形,我们有两个结论, 首先第一个就是角 a 啊,角 bdc 等于角 a 加角 b 加角 c, 下面这个角啊,角 bdc 指的是这个角,他等于这三个内角之和。还有一个结论呢,是跟边有关的啊, ab 加 ac, 哎,大于 bj 加 cd, 哎,大于这样一个有一个边之间的一个不等式的关系,那对于这个模型来说呀,用角度之间的关系,这样的体型相对来说会多一些。 好,接下来咱们一起来看一下这个结论是如何来进行证明的。如果我想证明这个角 b、 d, c, 还有角 a, 角 b、 角 c 之间的关系,那从目前这个图形上来看的话,不是特别的好证明。我们证明角啊,通常要借用三角形的内角和来进行证明, 那这里呢,题目当中没有给出三角形,所以啊,需要我们做一下辅助线,哎,那这个辅助线呢,我们可以这样连啊,我们可以连接 ad, 哎,然后呢,给他适当的延长一下啊,这里呢,用个红色的吧, 好,给他适当的延长一下,延长一下之后呢,这里就会出现两个三角形,分别是三角形 a、 b、 d 和三角形 a、 c、 d。 好,那在这两个三角形当中,角 b 和角 c 应该分别是两个内角哎,那么这时候的角 a 它被分割成了两个角,那这两个角呀,分别是左、右这两个三角形的一个内角,好,再观察这个角 b、 d、 c, 它也被分成了两个角,哎,那么左边这个角我们叫角一,它呀,应该可以看成是三角形 a、 b、 d。 的一个外角, 好,右边的这个角角二,它可以看成是三角形 a、 c、 d。 的一个外角。因此呀,这里我们就得利用三角形内角和这个定理的一个推论了。三角形的一个外角等于与它不相邻的两个内角之和, 好,那角一他作为一个外角的话,他应该等于与他不相邻的两个内角,也就是应该等于角 b 加上这个角 b, ad。 哎,这里呢,为了方便我再给他标两个角啊,这个角叫角三, 然后呢,这个角我给他叫角四,好,所以呢,我们就应该有角一,哎,他就应该等于角 b 加上角三,好,同样道理,角二也是一个外角啊,那么这个角二他就应该等于角 c 加上角四, 好,因此呀,这个角 b、 d、 c, 它如果等于角一加角二的话,是不是就可以分别用这个角 b、 角 c 直接来给它进行一个转化了啊,也就是说呢,这个角 b、 d、 c, 它就应该等于角一加上角二, 好,分别给它进行转化。角一等于角 b 加上角三,那么角二呢,就等于角 c 加上角四。好,那么这里这个角三加角四, 应该刚好就等于这个角 b、 a、 c, 哎,所以啊,他就应该等于角 b、 a、 c 加上角 b, 再加上一个角 c, 哎,这样的话,这个结论咱们就给他证明完毕了。 哎,注意啊,这里因为角 a 已经被拆成两个角了啊,中间有一条线了,所以咱们不能再用角 a 表示了,也要给他写成是角 bac。 好,这样利用三角形内角和定理的推论,也就是说,三角形的外角等于与他不相邻的两个内角之和。 哎,咱们就可以证明出这个模型关于角的这个等量关系了。好,那接下来第二个结论是边之间的一个不等关系,那这里啊,咱们肯定要运用到三角形的三边关系来进行证明。好,那这个三角 形的三边关系是什么呢?我们看在三角形 a、 b、 d 当中,应该有两边之和大于第三边。 哎,那么在三角形 a、 c、 d 当中呢,同样是有这个啊,两边之和是大于第三边的。好,那因此啊,我们可以得到 a、 b 加 a d 大于这个 b d, a、 c 加 a d 大于 c、 d, 但是啊,这样一来不行,这样一来的话,你这个 a、 b 加 a c, 你始终都没有绕开这个 a、 d 这一条边, 哎,我们呀,应该想办法把 a、 d 这条边呢,应该要给他消掉才行。好,那这样考虑的话,我们目前这种辅助线的方式啊,可能就不是特别的合适啊,那这里呢,我们稍微的给他修改一下,看一下这道题还有没有一些其他的啊, 做辅助线的这个方式,我们发现如果我把 b d 延长延长一下啊,那这样的话,也可以把这个凹啊凹四边形呢,切成上下两个三角形。 那在这两个三角形当中,咱们再来找一下,能不能找到他们这个啊边之间的一些等量关系啊?好,我来看一下,这里呢,我再给他画一个啊,把这个 bd 向上延长,哎,延长到这来。 好,这里这个焦点呢,我可以设为点 e 啊,好,这样的话呢,整个这个凹四边形就被分成了三角形 a b e 和三角形 cde, 哎,分成这两个三角形,那么分别在这两个三角形当中啊,咱们看一下他边有关的这个关系啊,那上面这角有关的,咱们已经证明完毕了, 给它清理掉啊。好,哎呀,这里被弄掉了,我再连一下啊。好,好,那么在三角形 a b e 当中,我们看啊,根据两边之和大于第三边,我们应该有这个 a b 加上 a e, 哎,应该是大于 b e 的。好,应该找到了这样的一个单量关系。好,继续啊,我们来观察你这个 b e 啊,它等于什么呢?它就等于 b d 加上 d e。 哎,因此呀,这个不等式,咱们还可以继续给它变形一下,也就是说这个 a b 加上 a e, 它应该是大于 b d 加上 d e 的。哎,我们得到了这样的一个 不能试,那上面这留给他清理一下啊,这种表示方式呢,不是很规范。好,继续。那么在这个小的三角形 c d e 当中,我们又有一个三边的关系,那就应该是 d e 加 c e 应该是大于 c d 啊, d e 加上 c e, 哎,它呢,应该是大于 c d。 好,这样一来,我们注意观察一下,这里呢有一个 b d, 这里呀有一个 c d, 哎,这样的话,我如果把这两个不等式相加,你看啊,这两个不等式都是左边比较大,那我如果把这两个不等式的左边加在一起,是不是一定应该大于右边加在一起,也就是这两个不等式,我可以给他进行相加啊,他相加之后呢,应该就是 a b 加上 a e, 哎,然后呢,再加上一个 d e, 再加上一个 c e, 它就应该是大于这个啊, b d 加上 d e, 再加上一个 c d, 哎,就得到了一个这样的一个不等式。好,继续咱们再观察一下啊,这里有一个第一,这里也有一个第一。哎,那这个不等式啊,其实跟等式类似啊,两边也可以同时减去一个相同的数啊,所以他俩呀,这里是可以直接约掉的。 好,那直接约掉,我们再来看一下左边,左边是 a b 加 a e, 再加 c e, 那这个 a e 加 c e, 大家观察一下, a e 加 c e 是不是刚好等于 a c 呀?所以呀,它就可以得到啊, a a b 加上 a c 就应该大于 b d 加上 c d, 哎,这样一来,是不是我们要证明的这个第二个结论,我们就给它正出来了呀, 哎,这里呢,利用的是什么呀?把一个四边形呢切成两个三角形,在两个三角形当中分别利用三边关系,哎,得到了两个不等式啊,这是一号不等式啊,这个呢,是二号不等式, 要把两个不等式相加,左边加左边一定就大于右边加右边,哎,然后呢,再进行一个适当的整理和变形,就可以得出我们需要的这个结论了。好,那这个结论咱们证明完毕之后,接下来咱们做一下关于这个模型的一些典型的习题。 首先二十四页的利益,将一副直角三角板按如图 图所示放置,使得两个直角的顶点重合。哎,那么角一的度数啊,这个角一,这个大的钝角啊,那三角板的三个角应该都是已知的,除了直角之外,在这个三角板当中有一个三十度和一个六十度, 那么在这个三角板当中呢,应该是有两个四十五度,哎,这个都应该是我们当做一个已知条件了啊。好,那现在既然想求角一,咱们刚学完这个燕尾的模型啊,我们看一下这个图当中是否存在着这个啊?燕尾的模型,那很明显,这里哎 会有一个燕尾的模型啊,虽然这个燕尾模型呢,不是那么标准,不是那么对称,但他确实是燕尾模型,所以啊,我们用红色线条把这个图形给他标出来啊,哎,就是这个,好,既然这里存在着燕尾模型,我们就可以利用燕尾模型的一个 结论。哎,那是什么结论呢?是不是这个三十度加这个四十五度,再加上面这个九十度,哎,应该等于哪个角呢?应该等于下面这个大的钝角,哎,这个钝角啊,我可以命名为角二, 也就是说呢,这个道题啊,角二他就应该等于三十度,加上一个九十度,再加上四十五度, 哎,这个算出来应该就等于一百六十五度,那角二如果等于一百六十五度,他现在求角一,哎,所以呢,角一等于角二啊,就等于一百六十五度,哎,那这道题啊,利用咱们这个结论 哎,直接就把把这个答案就可以给他求出来了,所以最后答案应该就是 d 选项。好,那这里呢,也可以进行其他的一些方式计算,但是 很明显啊,我们如果能记住这个模型的结论的话,直接计算应该是最快也最简单的啊,那当然,你用其他的,用三角形的角和去进行这个啊相加减的这个操作也是没问题的啊,啊,通过这道题,我们的目的就是让大家尽快的熟悉这个模型以及它的有关的结论。 好,继续来看二十五页的第一题,如图是一块不规则的纸片,已知角 a、 b、 c 等于角 d、 e、 f 等于八十度,呃,不要想啊,图上这两个角是已知的啊,这个和这个它俩都等于八十度,好, 则角 a 加角 c 加角 d, 再加角 f 的度数是多少?这个图上呢,仔细一看,有点像燕尾型,但是呢,他好像 像又不是燕尾型啊,哎,我们画之前学的燕尾型,他大概应该是长这样的,哎,应该是长这样的,那这里上面应该是有个尖那,但是这里很明显他就不是一个凹四边形啊,这里几个边啊,这里就相当于一个六边形了。 那这里我们又怎么样运用这个燕尾模型的结论呢?需要我们去添加辅助线了,一个六边形啊,咱们中间给它切一刀,其实就可以给它切成上下两个这种凹四边形, 那分别在两个凹字边形当中,都可以运用咱们这个燕尾形的一个结论,所以啊,这里就提示我们可以连接 ad, 连接之后我们就可以发现图当中就存在着这个燕尾的模型了。啊,好,我把 ade 连,很明显,上面下面这里出现了两个燕尾模型, 我就在这两个模型当中分别用一下结论是不是就可以了?哎,这里呢,角 a 和角 d 已经被分割开了,那咱们呐,为了看得清楚一点,给他标成这个标角一啊,这个标角二,也就角 a 呢,被分割成了角一加角二,那这个角 d 呢,现在就被分割成了角三加上这个啊, 这个角可能叫做角四。好,那么首先我们看在下面这个凹四边形 a、 b、 c、 d 当中,哎,这是一个燕尾模型,哎,在这个模型当中,我可以直接用结论,只用结论是不是应该是这个角 a、 b、 c, 它呢应该就等于角一加上啊,角三,再加上一个角 c, 哎,应该是有这个的啊,哎,一条线,你告诉我们它等于八十度了,所以这三个角度之和 就等于八十度。好,接下来在这上面这个凹四边形当中啊,也就是 a、 f、 e、 d 当中,也可以用一个燕尾模型的结论,那这里呢,就应该是这个角 d, e、 f, 哎,角 d, e, f, 它就应该等于啊角 f 加上角二,再加上一个角四,哎,他呢也等于八十度。好,这两个结论写出来之后,我们再来观察他跟我们所要求的这个式子之间有怎样的关系。 那这个狮子是四个角之和,我们这里啊,上面有三个角之和,下面又是三个角之和,我们看,如果把这六个角啊,全部加在一起,你看这当中的这个角一和这个角二相加,那就是这个角 a, 哎,那么这个,呃, 角三和这个角四相加,刚好啊,就是这个角 d, 那剩下一个角 c, 一个角 f 分别在这里,所以我只要把这六个角一相加,得到的就应该是我们要求的这四个角。 所以啊,那具体的步骤我就不写了啊,只要把这两个八十度一加,哎,八十度加上八十度,所以啊,最后结果就应该是一百六十度,所以这道题最后的答案应该就是 b 选项。 所以啊,在遇到题目当中没有直接出现咱们这个模型的时候,那就要添加辅助线哎,把它构造成我们所熟悉的这个模型,这样的话呢,就可以直接利用模型的结论了。好, 接下来再来看下一题二十五页第三题,如图,角 a 等于四十五度,角 b、 d、 c 等于一百三十五度啊,它, 哎,他是四十五度。 bdc 啊,这个角下面这个啊,他是一百三十五度,好,还给了一个角的倍数关系啊,角 a、 b、 e 等于三分之一倍的。角 a、 b、 d 啊,他是他的三分之一 啊,那这边呢,角 a、 c、 e 啊,他这个小的又等于角 a、 c、 d 的三分之一啊,这有两个三倍角之间的关系啊,求的是角 b、 e、 c, 求他的度数应该是多少。 那这道题当中很明显也存在着不止一个燕尾模型,首先,整个这个大的 a、 b、 d、 c, 它就是一个燕尾模型哎,那再来看上面这小的 a、 b、 e、 c, 哎,它也是一个燕尾模型,好,那, 那我可以分别在这两个燕尾模型当中啊,用结论了,首先在最外面的这个大的燕尾模型当中,很明显这个角 bdc 啊,写在这啊,角 bdc, 他就应该等于什么呢?应该等于这个角 abd, a、 b、 d 加上一个上面这个角角 a, 然后再加上右边这个角,也就是角 a、 c、 d, a、 c、 d。 啊,它呢,是等于一百三十五度的。好,那当然,这个角 a 呀,它已经告诉我们角 a 是等于四十五度,所以呢,这个角 a、 b、 d 加角 a、 c、 d, 我写了写下来啊,角 a、 b、 d 加上角 a、 c、 d, 他就应该等于这个一百三十五。减去这个角 a, 角 a 四十五,那一减应该是等于九十度的。好,得到这样的一个结论。 继续,我们在这个小的燕尾模型,也就是 a、 b、 e、 c 当中,又可以用一次结论啊,也就是呢,角 b、 e、 c 就是我们要求的这个角了啊,它呢,就应该等于这个角 a、 b、 e, a、 b、 e 加上一个角 a, 再加上一个这个角 a、 c、 e。 好,那求他应该等于多少度?好,那这里角 a 啊,同样是等于四十五度的,也就是说我只要求出角 a、 b、 e 加上角 a、 c、 e 就可以了。 好,那这里呀,因为存在倍数关系,我们呀,可以设一个未知数,我就设这个角 a、 b、 e 的度数为 x, 哎,设这个角 a、 c、 e 的度数为 y, 哎,也就是说,我最后要求的 是什么呀?我要求的就是 x 加 y, 哎,当然了,后面还得加上一个角 a, 也就是加上四十五度了。好,那这个 x 加 y 应该等于多少度呢?不要急,我们上面还得出一个结论呢,对吧?好,我们看一下,角 abd, 角 a、 b、 d 已知体条件给了啊,它呀,应该是等于这个角 a、 b、 e 的三倍 好,角 a、 b e 是 x 的话,那么这个角 a、 b、 d 很显然它就应该等于三 x, 同样道理,这个角 a、 c、 d 呢,就应该等于三 y, 所以啊,我们求出来的这个结论就告诉我们,三 x 加三 y 应该是等于九十度的啊,所以呢,这个 x 加 y 在这个啊,等式的左右两边同时除以三就行了,应该就等于三十度好, x 加 y 如果等于三十度,那这个是不是就可以求了,他就等于三十度加上四十五度好,所以最后答案呢,应该就是七十五度,哎, 所以最后的答案啊,应该就是 c 选项七十五度。所以啊,这道题相当于什么呢?把两个燕尾模型啊给他嵌套在了一起, 我们分别在两个模型当中,用结论再利用已知条件所给的这个角的一个倍数关系,哎,就可以求出最后的答案了。那当然我们求出的是 x 加 y, 也就是这两个角的之和,这里也体现了一种整体的一种思想啊, 当然了,有些人可以看到下面这个啊, b e, c, d, 哎,这里也存在着一个这个这个啊,燕尾模型,那在这个燕尾模型当中用结论其实也是可以的啊,有兴趣的同学这里呢,可以再去进行一个尝试。 那今天关于这个模型,咱们就一起练习,到这里咱们提示当中啊,关于这个燕尾模型还有更多的习题啊,大家呢,可以自行去进行练习, 我们下节课和大家一起来学习风筝模型,欢迎大家收看,如果喜欢我的课程,请关注明老师初中数学课堂。如果大家在学习中有问题,欢迎留言或者给我发私信,我们下次再见!
104明老师初中数学课堂
猜你喜欢
- 1066小玉老师
最新视频
- 36.9万圆梦数学 邪帝
















