拉格朗日中值定理断点如何得到
粉丝9.0万获赞45.8万
相关视频
 00:33
00:33 01:06查看AI文稿AI文稿
01:06查看AI文稿AI文稿这道题你还在用泰勒等价代换来解吗?今天教你们秒杀大法拉格朗日终值定力球极限视频最后有例题,务必看到最后哦!假如我们会了拉格朗日终值定力球极限,你看这不就是口算题吗? 接下来我们来了解一下原理。将基本公式带入函数,你看这两个从复合函数作差变成了内层函数作差,外层函数的 f 跑到求导的地方去了。从繁化减。海绵宝宝这个符号是什么东西?怎么算?他叫克西,需要用加逼定理来算。 我们假设克西在 g x 和 h x 之间,当 x 极限趋近于 a 十, g x 和 h x 相等,有没有感觉克西被夹在中间,所以克西与他们相等。上题目看到外层函数相同,都是一直接拉内层函数做 差,外层函数求导克西在两个内层函数之间,并且 x 趋近于零,得克西等于零,带入克西等于零,再化减,结果就出来。简简单单接下来是为大家准备的例题,有什么问题的小伙伴们在评论区评论哦!
1.9万海绵宝宝课堂 01:19查看AI文稿AI文稿
01:19查看AI文稿AI文稿大家好,现在我来给大家介绍微分中指定理的第二个,也是最重要的拉格朗日中指定理,他是这么说的,一个函数在一段 b 区间上连续在开区间上可倒的话, 那么在这个区间内一定存在这么一个值,使得下面这个等式是成立的,那我们就来证明它。首先我构建一个函数, gx 是这个样子的, 很明显啊, gx 符合在 b 区间上连续在开区间上可导,那么我们观察发现啊,两端的函数值是相等的, 那这样的话,明显对 gx, 我们就可以利用我们已经证明过的罗尔定理,在区间上 一定存在一个直科赛,使得 g 科赛一瓶是等于零的。那我们现在对 gx 求导, 然后带入存在的这个值和赛,我们就会得到好,得到这个等式之后呢,我们把 b 减 a 给乘过去,这就是我们证明之后的拉格朗日中制定理,你听懂了吗?
1162考研数学 02:21
02:21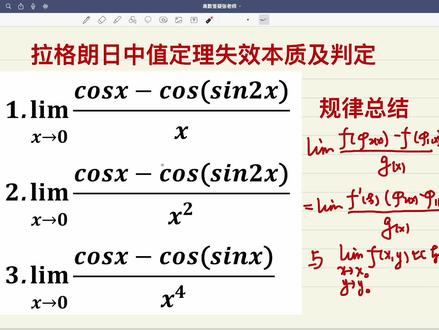 26:02查看AI文稿AI文稿
26:02查看AI文稿AI文稿来讲一下这类题目呢,有的用落单法则还可以,有的呢就是会比较麻烦啊,要用这个 罗布达法则,嗯,有的用其他的方法来做。那我这里面重点来讲一下拉格朗的中字定理呢,咱们说有时候会失效,那么他失效的本质是什么?到底怎么判定什么时候能用,什么时候不能用?是咱们讲一个重点,就是重点总结下的一个规律啊。 那咱们知道用拉朗中中字定理呢,咱们说的总是会出现一个这个地方有个可 c, 然后这里面本身呢有个 x, 这时候大家就感觉我这个是 s 全于零,根据两边加准则呢,通常比如说啊,可 c 也是全于零的, 那么这时候这个地方就感觉像一个二元函数极限,那和这个极限有什么样的一个关系?那么咱们它的本质到底是什么?咱们下面具体来看一下啊, 我先把这个规律呢,先简单的稍微说一下,然后咱们再具体的结合题目再来具体解释啊。 嗯,咱们说的什么时候用拉朗宗定理呢?咱们通常是这样子,就说的我这个地方呢是有一个叉的一个结构啊,这个地方是有一个叉的叉的结构, 同时这个地方是 f, 这个地方也是 f, 他们是对应相减的,所以这时候呢,咱们说两边都是 f, 那我这个地方就设成是 ft 这样的这种形式。 然后接下来呢,咱们就是来看一下我这个地方呢是一个 fi 一 x, 这个地方是个 fi 二 x, 把这块就看的是两个端点, 所以这样话呢,用拉朗中定理就等于函数在某点的倒数乘以呢,他这块对应相减就可以了,就形成一种形式。那么这个可 c 呢?是介于咱们两者之间的,写完以后咱们接下来求极限。怎么求啊?那咱们求极限是这样的,如 如果这个极限是存在的,这个极限也是存在的,那咱们就直接带出算出来就可以了,每部分极限都存在,就乘起来就可以了。那有的同学就是有疑问,他说的你这个地方求极限是对于可 c, 比如说,比如说区上以零,你这边求极限的是 s, 区上也零。 我原来是一元函数的极限,你给我猜成两个,这样能行吗?咱们等会我去解释,这样做是可以的,完全可以这么做的啊。 这是说的第一种情况,那咱们下面来说,呃,一般的规律啊,咱们一般的规律呢?就说如果这个极限啊,这个极限假设他是等于一个常数,这个常数只要不等于零,后面极限有没有有可能存在,也可能不存在。我不管,他,只要这个极限是 菲灵的一个常数啊,是菲灵的常数,那么这时候拉格朗中定理一定是可以用的,就是我写的这里的第一种情况, 一定是可以用的。为什么?因为你这个 cc 已经消失了, cc 消失了,那你剩谁了?只剩这 x 了,只剩这个极限了,那这个极限存在就存在,不存在就不存在,就完事了。因为咱们说飞行的这个极限呢,本身就不影响它本身的极限,这是说的第一个结论啊, 然后再来说第二个结论,如果这个极限等于零怎么办?如果这个极限等于零了啊,咱们刚才说是不为零的时候,不为零是不影响整体极限的,但如果这块为零的时候,为零的时候,后面这个极限到底存不存在呢?那么这时候就分成这个极限可能是一个 存在的,如果存在,刚才说两个都存在就带入呗,那极限就存在,答案就是零就完事了啊。但是有的时候这个地方不是 a, 这把不是 a, 可能是一个什么,是一个无穷大,要是无穷大的话,那咱们知道这时就出现了什么零乘无穷大,零乘无穷大,这时候极限 到底存不存在呢?就复杂了。现在这种情况下啊,在零成无穷大这种情况出现以后怎么办?咱们就是来比较这个地方跟这个地方他们两个到底等不等价的问题,如果等价的话,可能用两边加准则,这个中字定理还是可以用的,但如果不等价的话就是不能用了。 那我这里边也稍微说了一下啊,这是刚才解释的,说他要等于零的时候,就是看剩下的那一部分极限是否存在,要存在都给他带住就完事了啊。关键难点和重点就是这个地方, 这个地方如果出现了,这把是无穷大的话,刚才出现了就零成无穷大这种形式是不是就可以转化成呢?这个地方到底等不等价?如果等价,我刚才说的通常是考虑两边加准则,一般是能得出来的,但是如果要是不等价的话,那么两边加准则就加不紧了。 具体是什么样一个情况,并且这块是怎么处理?那咱们具体来拿题目来看一下啊,咱们先来看这个第一个题目,第一个题目呢,咱们说的,你看我这里面这个地方是 f 减去,不是扩散减,扩散中间是个减号,对不对?那自然我就想到设这个 f t 等于扩塞 t 了, 而这个 t 就是介于他们两者之间,这是很自然的。然后接下来呢,我就用中文地理等于函数在某点的倒数,这不某点的倒数吗?乘以他俩对应相减,就写出这一步了。 学这一部后,咱们咱们接着来啊,这个地方极限他不就是一吗?我就裂开这个地方的极限,是用上面等价替换,这块极限就是二吗?一减二,那我整个这个地方极限,这个极限就是负一了啊,这极限是负一, 所以这样话呢,我这个极限咱们说是负一,咱们再看这个极限本身等于多少呢?是零,那零乘负一就算他就完事了,就可以拆开。那我再解释 为什么刚才说有东西说你这款是对可 c 球极限哦,你这是对 s 球极限哦,凭什么能拆成这两个极限相乘?那我解释一下啊。 嗯,这里面咱们来先来说一下,如果这个可 c 呢,咱们看成是完全独立的,就是我看成完全是 s y 啊, s y 全于零,这 s y 咱说有什么特点呢?我看他这个二元函数啊,我特意把可 c 写成 y 了,特意把可 c 写成 y 了,那么这时候他有个什么特点呢?我说的 x y 是相互独立的, 如果这个极限存在,这个极限存在的,咱们讲是什么意思呢?二元函数讲极限存在,是不是以任何方向任何方式就是这块画的啊?任何方向任何方式拐道弯的趋向于他极限都应该是相同的,是这个意思, 咱们来看这个表,什么意思啊?这个来说呢,它跟二元函数的极限是不同的, 因为什么呢?因为这里面多了一个限定,这个可 c 它不是独立的,它是介于 x 和 c、 r、 s 之间的,是这个意思 g 之间的。那么这样话就说明什么意思呢?从我图形当中看啊,假设 x 和 c、 r、 s 图像呢?就是我现在画的这个图形, 怎么画?咱们等会再去说啊。这个地方假设画出来了,画出来以后呢?我这块指的是什么意思呢?就是指的是在这样的一个, 嗯,可 c 啊,可 c 只能从这样的一个方向取向于零,从这里取向于零,因为咱们知道这个可 c 啊,这个可 c 总是介于介于这个地方的 x 和赛 r、 s 之间的吗?那我这边的话, s 曲项于零的时候,他曲项于零,这边也曲项于零,根据两边肩夹准,咱们知道可 c 一定是曲项于零的,所以这样话呢,你说这可 c 曲项于零,是在我这个地方画的红色这个地方,这个地方曲项于零,同时在这个地方也是 圈与零的,那么这样话,也就是说我在这些特殊的这样的一些路径,在这样线条件下,圈与零,那和你如果这块极限存在的话,那一不一样,一定是一样的。你这边任何时候极限都是相同的,那我这个地方特殊的这样的路径,极限一不一样,一定是一样的。像我这样红色的这样的地方, 极限一定是相同的。这样话,也就是说只要你看成 sy 完全独立的话,那我说的只要这个极限存在啊,我说的意思就是只要你这个极限能够算出来,我现在算了等于零了吗?只要这个极限存在,那特殊的限定的条件下,极限也一定存在,就是我写的这个第一个结果啊,就是这个第一个结果, 二元函数极限存在,那么有任何有限有限定条件的二元函数也一定是存在的,就这个意思,但是反过来,反之不一定成。 就说这个边的存在能不能保证这边存在呢?那不一定,因为有的时候只有这个地方存在,并不能保证其他的方向 或方式是存在的,就这个意思。现在我这里面特意这块就写了一下,二元函数极限即使不存在,那么有约束条件的这个二元函数就是这个极限呢,可能是存在的,就这个意思啊,这个地方要注意一下。 那咱们下面呢就是,呃,来看一下,我把现在题目呢稍微改一下,咱们看一下第二题如何来做啊?第二题, 嗯,这个第二题呢,我把刚才的那个地方的 x 改成加了个平方,跟刚才的区别分子处理一模一样,所以只是这块多了个平方。多了个平方,我现在怎么去呃,处理的啊?我现在呢就把这个平方呢,我就给它拆开, 拆成两个,我这边稍微写一下啊,就把这个平方啊拆成这边这个 x。 那从这里面咱们看到刚才这个极限不求完了吗?这一裂开,刚才说这个极限不就是负一吗?这极限是负一,然后剩下的呢就是这个极限了, 那现在就变成这个极限到底存不存在的问题?那咱们先给他回到就是完全独立的二元函数极限看一下啊,如果要看成完全独立的二元函数极限,那我这块就写一下 x 取消于零, 我这个可 c, 我就帮写成 y 吧,这个 y 也全于零,因为这个可 c 呢,是介于这个 x 和 c r r s 之间。什么意思?就是这个可 c 啊,可 c 是介于这两者之间, 在 h 区域零的时候,这个是全于零,这个也全于零,用两边加整个可 c 是一定全于零的啊。去弄的话就暂时先写成歪,写成歪的话,那这个地方我们看到的话就是塞也歪了, 这个地方就是 x, 那么这个地方呢?咱们说的可以去验证,要学了二元函数极限可以去验证啊,这个极限一定是不存在的,因为我这里面取 y 啊,我可能取 y 等于比如三 x 啊,或者是呃,其他的一些形式啊,那么这时候这个能够得到这个极限,不同的路径,不同的路径极限他可能是不同的,就这个意思,所以这样的话,得到这个这种二压住进不存在。那咱们刚才说了,我这个地方的极限 不完全是和二元函数的极限是一样的,即使你不存在,我也可能存在啊,也可能存在,那到底他存不存在呢?也就说咱们现在看我这个地方的只能是从这个方向取向于他啊,在这个方向取向于他可不可能存在呢?咱们下面来看一下, 咱们要做题,比较简单的话,咱们就这样子啊,你就是看这个地方,一个是 x 这个地方,一个是晒二 x 啊,就是我可睡,这是可睡的一个范围,可睡在这样的一个范围内, 但是这个范围到底谁大谁小咱们不清楚,不清楚你也不管,不用管他啊,所以这样话呢,我加个赛也可 c, 那你这边也加个赛耶,赛耶二 x 这玩意也加个赛耶 x, 就这个意思。然后呢,你这个地方要怎么样?要比 x, 那我把它也比上 x, 那这地方也比上 x, 这块也比上 x。 这个地方咱们能够得到这个极限来说就是等于二的,而这边的极限是等于多少呢?等于一的,所以从这里面看到,哎,两边极限都不同哦,比如说我这个来说,应该是介于这两者之间的,结果他介于一和二之间,介于一和二之间,那就是, 嗯,夹笔准则没法用了吗?所以呢,就是没有办法去判定啊,这个我是比较粗糙的,平时做题那么很粗糙的去想一下就可以了,说明两边夹呢是不好用的,我说的就这个意思,那我下面我再详细的来说一下啊,也是从大家的这个 呃,很严密的理解上咱们来说一下。首先我先说下我这个图形最怎么画的,我怎么知道赛 rx 就比这 x 大,我这会稍微的来解解释一下啊。 那么这个地方说的,当他俩大小我判定不了的时候,就把这两个函数怎么样?做一个叉,现在我在这个地方我就设一个 gs, 等于他俩做叉,做完叉以后呢,我就是,嗯,利用倒数,这个倒数等于他, 然后我把这个导数呢取极限,这个极限很显然是等于负一的,那么极限要小于零,咱们根据饱耗性就会存在某一个领域,在那里 里面对应的函数是小于零的,所以呢,这样话就是根据饱和性就得到这个小于零,倒数小于零得到函数单调递减,既然递减的话,那么咱们在区域零加的时候,那么这时候根据递减就得到这个关系式,而既定是零吗?这样话就得到这样的一个关系了啊, 二可 c 是基于他们两者之间,所以我就写出来了这个关系是同样的 s 幺大于零的时候呢,呃,圈于零减的时候也得到另外一个关系,那就是我写的这个关系啊,所以这样话呢,在这两种情况下, 为了得到咱们刚才的那样的一个两边加,现在只有这样子啊,我把这个地方呢,就两边都取正弦,咱们正弦是个单调函数,单调递增的取,这样话呢,不等式,方向不变,这等就不等式,方向不变,就是这个意思。然后咱们写到这以后呢,我接下来咱们再我再接着来写啊,这时候咱们说的 我要比上 x, 由于 x 呢是一个正的,那我两边都比上 x, 都比上 x, 方向是不改变的。然后这个地方我们看极限,这个极限就是一,而这个地方的极限呢,它就是等于二的, 这节就是二,所以这样的话说明用两边夹准则是夹不住他的,得不到这样的一个极限,得不到他啊。那么同样的道理,相遇零减的时候呢,把他方向改变一下,这完全完全是一样的。只是说这个地方在除上 x 的时候啊, 因为单调递增方向不变啊,方向不变,但是除以 s 小于零了,这会就方向改变一下,改变以后呢,这个地方也是仍然他比上 x, 这个极限就是二,这个极限呢,比上 x 极限是一, 也是就是夹不住,相当于啊,两边夹不好使,所以呢,从这里面看,就是从这里面就得到了这个拉个朗字方法呢,是完全 失效了,用两边夹也仍然不好使。咱们通常是是说一有,可是一有 x 的时候就有,这的时候就看两边夹到底好不好用,那么这个 为啥失效呢?咱们再看他这个本质啊,这个本质就是因为这个赛二, x 和这个就是这个里的赛二, x 和这个什么和这 x 之间怎么样啊?他不等价, 如果等价的话,两边加应该就是一般来说都是可以用的了,现在是不等价,不等价就不能用,就这意思。这样话也说,我把这个题目如果这块稍微换一下啊,我给他换成什么呢?我就把这个地方把二给他划掉,就是 x 的时候,那就是可以了。 我,我相当于,我是说这个意思啊,我用绿色把这个地方二给他划掉,他如果这个二要是没有的话,那我这个地方他俩就等价了吗?那我这个地方二都没有了,这个 二没有了,这个二没有了,那这不就是一了吗?这是一,这也是一,那两边极限都是一,那得到中间极限就是一,所以这样话呢,这时候就能够得到这个答案了,这就说明我如果把这个地方要是改成 x 的时候,那么他是等价替换。 呃,两边加准则是可以用的啊,拉朗的中文定律并没有失效,就说这个意思啊这是,呃,这个题目, 那么下面呢,咱们再来看一下第三题,第三题呢?嗯,刚才说失效了,失效怎么办?只能用其他的方法, 那我这里面写了有两种方法啊,第一个就是用洛洛塔法则,上下分别求导数,求的是求彻底一点就可以了。那么这时候咱们能够看出来这个地方呢,我就给他裂开啊,能裂开就裂开,这个极限就是负二分之一等价替换。然后咱们再来看这个地方呢,我把这个地方可以等价替换,这个地方等价替换成 二 x, 那和这二 x 呢?就约掉了,这种状就是一没有了,剩下带入这块带入就是二,就是这个二了啊,就算完以后就可以了,那么也可以用什么呢?用这个公式 扣塞,减扣塞等于负的二倍塞塞,所以这样话呢,我就是用这公式,用完以后呢,咱们看到这个地方极限不是零吗?这两个极限都是零,所以既然极限都是零,我就把这个地方等价替换,就把它划掉,划掉完以后呢,我把这个分母给它裂开, 尽量让每部分极限存在。那么看到这个地方的极限,你分别看,这极限不就是三吗?你这块是一吗?他俩结合,他俩结合就是二,那么同样的这个地方呢,一减二是负一,所以呢这样算也可以, 这是在失效的情况下,咱们来进行处理一下啊,下面咱们再来看一下啊,第三个,第三个我为了做对比呢,我也特意这个地方呢,就是,呃, 把这个地方改成这个就是赛 x 了啊,不是二 x 了,已经是二 x 了。那我放了一个是平方的,一个是立方的,一个是四次方的,咱们做一个比较,那么这款是二三四的时候呢?那咱们看到啊,我做的时候仍然用 拉个朗中定理,跟刚才处理方法完全一样,这边是完全一样的,然后接下来做我怎么样呢?我就是说,呃,这里面有一个大家可能应该比较熟悉吧,用拉个朗中定理, 不是拉拉能力,就泰勒公式啊。这个大家都知道,这个是等价于六分之一 s 立方的,要是没有学过的话,你这个地方不用去背他也行。我就是说适当的组合,组合完以后 是什么呢?就是这一部分的极限,你要没有不知道这个等价替换,你就把这个组合完以后呢,用落大法则去算。 说完以后呢,会得到这个极限呢,是等于零的,这个极限是零,前面这个极限呢也是零,那一乘答案就是零,这是平方的时候,另一方的时候呢?那我一样的,所以这个地方的组合还是把这个上面这个带进去,那这个地方极限就变成六分之一了吗?那前面极限是零,刚才说能带住存,带住了就可以了。 那我现在要是四次方怎么办?四次方我还这么组合,还这么组合,发现这个地方的极限呢?因为刚才说上面是三次方吗?三次方,下面四次方,那这块极限就是无穷了呀, 这块是无穷,这块地方极限是零,那么说零乘无穷大是没法做的,极限符号也不能拆开,所以呢,这样话就说明我这个地方是错的,这样不行,这块不行怎么办?那我现在呢就给他适当的去组合,那这个组合就有一个技巧啊,当如果这块出现无穷大的时候,咱们怎么组合呢?我一定要组合,让 这一部分的极限是一个固定的数,因为我刚才知道分子是有立方,那我就给他个立方,那这块极限不就是六分之一了吗?让这块极限这个数,然后剩下的东西都给到前面去,给到前面去以后呢?那我就算这个极限,那这个极限咱们刚才讲了啊,这个地方 咱们说的能不能够用这个定理来做,接下来呢?咱们说的你先不要说用不用两边夹,你首先看一下我这个地方的 区间,就是这个啊,这个 s 和这个赛他等不等价,那咱们看他俩明显是等价的呀, 既然他俩是等价的,就是这个塞 s 等价于 x 啊,他俩等价,那咱们说的两边加准则应该是可以的,所以下面呢,咱们就用两边加准则。那么我这里面呢,咱们说刚才也是说用的时候呢,嗯,因为这个可 c 啊,这个可 c 是 介于他两者之间的,那这样话 say c, 这个 say c 就是介于 say x, 这玩意儿也加个 say 嘛, say c, x 就介于他们两者之间这玩意儿的大小关系,咱们说的平时要做客观题,不用去写也行啊。 然后这时候呢,咱们说的把这个地方再怎么样,再除以 x, 就能把它除以 x, 这块也除以 x, 这块也除以 x, 那么从这里呢,咱们就能够看到这个地方,刚才说你看这几线不就是一了吗?这个地方咱们用等价替换,是不是这款极限也是一啊?两边极限都是一的,中间极限也是一吗?就这样话就说明这个地方的极限是能够算上是等于一的啊,要是严格来写的话,那就分成呃, 零点的右侧,然后有什么样的不等式关系?然后这个地方是怎么写的,还需要零点又怎么写的啊?这样写就稍微慢一点,但是呢会 更严密一些,就这个意思,这是四次方的时候啊,那么这个地方的规律呢?我把这个我再说一下啊,前面刚才已经说过了,那我刚才说的重点是什么呢?就是说的 如果这个地方前面极限是零,这个地方极限是零,后面这个极限出现无穷大了,就什么意思呢?出现了零成无穷大这种类型的时候,咱们马上就给他转化成比较这两个范一范二他们两个这个地方是否是等价的转化成这 如果等价的,咱们刚才说的就考虑两边加总则得出来就行了。如果不等价的时候,不等价的时候能不能用呢?那咱们说的一般来说是不能用的, 但等价的时候,等价时候,刚才说的用两边加准则啊,那如何能用呢?那我这个地方我也稍微的来解释下这个地方如何来 用啊?由于这是无穷,咱们刚才那个题目咱们是怎么去做的?我就是这样子,我把这个地方的 g x 啊,这个的 g x 就拆成两部分,拆成一个 g 一 x 和一个 g 二 x, 就这样意思,然后呢我保证什么呢?这一部分 这个 g 二 x 跟他放到一起,这个极限呢是一个固定的数,因为你极限只要是无穷大的话,我一定能做到这一点的,所以这个地方极限就是个固定的数,那这不多了一个 g e x 吗?那我这个 g e x x 再怎么办?就和这个前面的,刚才不是有 f 到可 c 吗?有一个,这个和谁呢?和这个 g e x, 我就变成求这个极限就可以了,就看这个极限到底存不存在。而这个地方的极限呢,就用两边加准则,所以这个地方一会咱们再稍微的详细看一下。啊,那我这个地方呢? 啊,还有一点我也说一下,嗯,先把这段看完吧,就是回到这里来啊, 我把刚才那具体解释一下,我刚才就是说把这个这个地方的 gx, 我刚才说拆成了两部分吗?拆成了一个 g 一和 g 二,那我刚才说的如果这个极限是存在的, 我就给他拆成这部分基因,我就凑出来一个基因存在,然后余下的。这话我说的余下余下谁了?余下了这个吗?那这个咱们说的总是介于什么呢?因为可 c 刚才说可 c 是介于发一和发二之间的,那这样话呢,我说的这个极限就介于这个 和这个之间,就基于他们两者之间,那么这两者之间,咱们知道 f 一 x 又等价于 f 二 x, 在他等价的情况下,那这两个极限呢,就会怎么样?一般情况下会是相等的啊, 一般情况下会相等,因为那个 f 通常他是一个连续的,并且呢就是说的呃,他可能是一个单调的之类的,所以呢一般来说他是相等的,所以这话就是我这里写的,如果他们要是等价的话, 等价的话,那么通常这两个极限是相等,这两个极限相等,两边极限相同,那中间就有同样的极限呗,用两边加准则就可以了。 那么如果这个地方要是不等价,不等价,通常来说他们两个极限就不相等,就相当于夹不住啊,夹不紧,所以这时候呢,就是拉个郎中的,你就失效就可以了。那么这里面呢,我也特别说明另外一点啊,就是我这里面刚才我说话写了我没有提到的, 咱们在看的时候呢,就是说,呃,这个地方啊,我这个地方稍微提一下,就 就是说咱们有时候这个范一和范二这地方是不等价的啊,不等价的,不是说不等价就一定拉朗诵中定理失效,不能这么记得,即使他俩是不等价的,但是如果这个极限 和这个极限,只要他们两个都存在啊,这两个都存在,那么拉朗日中定理是可以用的。咱们最开始第一个题不就是吗?第一个题目分不上 x 的时候,那个地方根本就不等价呀,是不是?但是呢,咱们说拉朗日中定理是可以用的啊,这一点需要注意的,这是这个地方,那 我再举最后一个例子啊,咱们这个就给他稍微的组合一下,就是我这里面的这个,你看我又给他改成五次方了啊,咱们刚才不是四次方,咱们做过了,我改成五五次方,这个改成五次方以后,我说怎么做呢?那咱们说的你如果就是这 这么样去看的话,如果这么看的话,那这个极限,刚才说分子这块极限他不是等价于六分之一 s 立方吗?那你把他带进去以后,那整个的这个地方这个极限就会得到,他是无穷, 这就是变成零乘无穷大,因为前面极限是零吗?零乘无穷大这种类型的,那这种类型咱们说的怎么去做啊?那咱们的技巧是什么呢?因为刚才说这个地方既然你等价于六分之一还是立方,那我现在就把分母放个立方,然后余下的余下就放这了,放到这以后,咱们说这个极限 能不能够去求?能不能去求?那我这里面咱们也是观察,那我刚才说的这个地方的 x 和 cs 之间是什么等价关系?他俩等价的话,那应该能用两边加准则啊,这个极限应该是能够求的,那咱们下面就来看一下啊。 那我这把就简单的写了一下,我说可 c 呢?这个可 c 是介于他们两者之间的,那我 c 可 c 呢?把两边都加 c c 的介意 c x 和 c c x 之间,那么这是要求这个极限怎么办?那我说这个极限就介于这个极限,把上面这个除以 x 平方, 这个也是把上面对应的也出牙齿平方,就介于他两者之间就可以了。那么从这里面咱们能够观察出来,我这个地方如果就是等价替换完以后,是不相当于就是 s 分之一的极限,对吧? s 分之一极限本身来说,这个极限就是等于多少,就是等于无穷大的啊,就等于无穷。而这个地方也是一样的, 用等价替换,等价替换化解完以后就是 s 分之一的极限,那这个极限呢?也是无穷,这边是无穷,这边是无穷,那我这个地方极限怎么样啊?他也就是无穷, 你这两边都是无穷了吗?如果他要两边都是正无穷,那这个地方就是正无穷,他要两边都是负无穷呢?他对应的也是负无穷。所以这样话呢,就是相当于一个 这个地方极限。刚才说了这个地方极限咱们知道是等于六分之一吗?六分之一乘成一个无穷大,那最后答案就是无穷大极限是不存在的,那实际上极限是不是不存在的?那指定是啊,咱们刚才不是算了这个四次方的时候,咱们刚才算了那个四次方的时候,极限在这呢, 四次方极限的时候算完不等于这个吗?刚才是四次方的时候啊,这个极限是固定数,那我要五次方怎么办?我把这个地方就相当于再乘以 s 分之一吗?那一个长数乘上一个无穷大,最后答案确实是无穷大就可以了啊,这个地方看是否完全。 呃,清楚了,讲的比较啰嗦一点,反正大家尽量给他搞懂啊。这会咱们就讲这么多。
344高数答疑张老师 00:21查看AI文稿AI文稿
00:21查看AI文稿AI文稿恋爱脑带你学高数之拉格朗日终止定力,在函数连续且可导的一个区间内,至少有一个点的斜率与区间首尾相连的直线一致。我的意思是,在人生这段旅途中, 你一定会遇到一个跟你斜率相等的人,陪你一起走下去,度过余生。听懂了吗?
10.7万今夜不挂科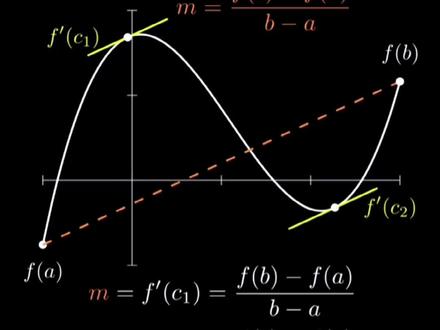 00:33
00:33 13:24查看AI文稿AI文稿
13:24查看AI文稿AI文稿大家好,今天呢,六姐给大家录制的仍然是今日考题,今天呀,六姐要讲解的是拉格朗日中职定理的相关考题。拉格朗日中职定理的考题的话有两种, 一种呢是证明不等式,那么第二种呢是求极限。那么今天呀,我们先来讲讲拉格朗的终止定理如何去证明不等式,我们来快来看一下今天刘姐给大家准备的这道题, 题目是说让你去证明这个不等式,我们首先发现啊,这个不等式他是一个,我们观察一下,他是一个双向不等式,他有两头,那不等式的话,我们再来回顾一下不等式他的一个方法有几种?证明不等式,我们说 我们主要有两种方法,第一种方法就是构造一个辅助函数,利用他的单调性,利用单调性去证明不等式相当于导数的一个应用。第二 个就是我们的拉氏定理啦,或叫做拉格朗日定理。那,呃,这个题的话,利用单调性也可以做,利用拉格朗日也能做啊,那我们看看单,所以如果单调性不能做,那你就去考虑一下拉格朗日,如果拉格朗日你做不出来,那你就 用一下单调性,看这两种方法你哪个更熟,你就用哪个就可以了。那这个题的话,呃,今天我们不去讲,那他如果要使用单调性的话,你要构造两个函数 去证明出去证两次,呃,首先这个不等式,你要构造一个辅助函数去证明他的单调性,然后去证明他,还有一个就是前面这一个,所以你要构造两个函数,如果利用单调性的话,要构造两个函数去利用单调性去求解, 那比较复杂一点对不对?那我们就利用我们的拉式定理,看一个定理就把这个双向不等式全 全部搞定了,所以以后大家看到双向不等式,可以优先去考虑一下拉式定理,如果拉式定理不会的话啊,不可以做的话,再去考虑一下单调性,就是在双向不等式的时候, 那好了啊。说到拉式定理,我们来看一下什么叫做拉格朗式定理,如果这一块不需要听的同学可以直接跳过去啊,有需要的同学我们一起来回顾一下。 那拉格朗日终止定理的话啊,就是这个东西,定理一,如果一个函数满足这两个条件,所以啊,他只需要两个条件就可以了, 在 b 区间上面,两区连续开,区间上可导,所以简称 b 连开导一样的,跟我们的罗是不是一样的呀啊?罗尔中指定的前两个条件是不是一样的? b 连开导,他没有第三个条件,他只有这两个条件,罗尔定理还有一个 f a 等于 f b, 对不对?那么他 说至少一样的,也是至少至少存在一个点可塞属于开区间,使得 f 撇可塞等于他。看到他有没有很激动啊?是不是很像我们的斜率的一个公式,我们说直线的斜率就等于 f x 一减去 f x 二除以 x 一减 x 二。这里说一下, 你这里 f x 一减 f x 二除以它,你或者是你用 f x 二减去 f x 一都可以,但是一定要保证上面是一减二,下面也是一减二,上面是二减一,下面也是二减一就可以了啊,所以同学们不需要去纠结到底是 f a 减去 f b 啊,还是 f b 减去 f a, 没有大小关系的啊。呃,如果你想用大的减小的也可以,用小的减大的也 ok, 但是要保证上下一致就可以了。这里讲一就讲一点这个。那好啦, 那相对于如何种植地理地理来说的话,拉格朗日定力好像更容易满足,因为他只有两个条件就可以了。那我们看看拉格朗日的几何意义是什么?几何意义?我们说了这个的几何意义,既然是斜律的话,那这是两个,这个是这个曲线的端点。 呃,它相当于是这个 a b 直线的,它的斜率是 k a b, 它的意思就是说在这个曲线当中会存在某一点可塞一或者是可塞二,至少存在这么一个点,它的切线的斜率会跟这个 a b 直线的斜率是平行的,平行直线平行斜率相等。 所以啊,他反映的是一个平均变化率和曲线上某点的变化率的这么一个关系。那其实呀,拉格朗的定理呢?我们给他再补一个条件,如果 f a 等于 f b, 我们就 能推出来这一坨,就等于零了,所以直接也能推出来 f 卡,可上海等于零,所以通过拉格朗日也能推出罗尔终止定理,再加一个条件就能变成罗尔终止定理了。好了,这是拉格朗的定理。拉格朗的定理,再讲一点额外的, 他又叫做拉氏定。拉氏定律啊,我们有同学很很搞笑,给他弄了一个,起了一个名字,叫做什么拉氏定律。所以拉氏定律指的就是他啊,就是我们的拉格朗日充值定律。那好了,那我们一起来,回过头来, 嗯,看一下啊。哎,点这里,那我们一起来用我们的拉屎定理来做一下这个不等式。那拉屎定理,我们,呃,把刚刚那个拉屎定理写一下,他说的是 f 撇克 side 等于 f b 减 f a 除 b 减 a, 最关键的是我们要去构造这么一个函数,对不对?去构造,去找到这么一个函数,只要你找到这个函数,他两个条件必必连开到,这个是肯定符合的,关键,我们只要找到这个函数就可以了,然后就立刻很容易满足,立刻就得出这么一个结论。 对,那好,那我们现在看到这个不等式,我们首先要找到这个函数啊,还要想找这个函数,呃,有一个题也叫做这里是一个关键啊,就这个东西, f b 减去 f a, 两个函数值相等,只要出现两个函数值相等,立刻你就知道这个函数是谁了,所以通过 f b 减 f a, 立刻找到 f a 是谁。那我们来看看这个题当中这里的话,呃,那也跟函数有关的,这个是 x, 这是 e 加 x, 这是 x, 它更多的像呢,是变量,跟函数有关。哎,我们就往我们的五大类基本处呢,函数反对秘制三,那这里有个对数啊,所以我们在考虑这个函数会不会是一个对数函数 有了这个思路,但是我们说函数要是函数值相减呀,这里只是一个很单纯的一让,一加 x 没有减, 没有减的话,也许它减的是零,你可以给它添个减。那浪,要想形式统一,都是 f f 的形式,你要把零也算写成 f f 的形式,那浪谁等于零呢?那就是浪一啦。 那 ok, 此时我们的这个 a 和 b 就出来了啊,我们这个函数就出来了,它相当于可以看作是我们的 b, 它相当于可以看作是个 a, 所以我们的函数解析式就是有了 fx 就等于他们相同的这个东西 long, 所以 long 这些不同的地方变成 x l, ok, 这个函数就已经找到了。函数找到,我们要找他那个 b 区间, b 区间是什么呢? b 区间就是你这里的 b 和 a, 所以 x, 你要构造的函数就是 f x 等于 long x, x 属于小到大,所以属于一到一加 x, 因为 x 是大于零的。 ok, 我们就找到了这个函数,听明白了吗?这个函数找是关键啊,怎么找?就是通过这里的 f b 减 f a, 你要去找一个函数 直相减,那你看看,这里面只有一个函数浪他,那你要给他去补一个减,于是这样子就找下来了。呃,这里怎么有同学很纠结的问我说,浪他减,浪他为什么等于浪他?如果你实在理解不了,我教你个小技巧,浪这个东西减浪这个东西,这个函数怎么去找呢?相同 的地方挪下来,不同的地方全都变成 x 就可以了,那其他的这个区间,这个 b 区间,那个区间的端点,就把这些不同的地方挪过来就可以了,就这个意思,明白了吗?嗯, 这里是构造函数,如果构造函数你会了的话,那我们应该怎么办呢?先把这一坨先删掉啊。假如你已经会了构造函数了,那我们怎么通过?呃,构造那个函数使用拉格朗日把这个题求出来呢?下面的一个分析方法, 你写下分析方法,我把它叫做倒推,就从已知往回推,就是倒推去倒推,从结论入手。 从结论倒推,倒推的意思是从结论倒推,从已知入手。好,我, 那我们一起来推一下,我们刚刚这个函数已经构造出来了, f x 等于 long x, x 属于的是一到一加 x, 我们是通过那个 f a 减 f b 给它构造出来的,刚刚对不对?那我们再对这个函数使用一次拉格朗日,就是 f 可 f 平安可赛 等于 l 一加 x 减去 l 一除以一加 x 减一,也就是 l 一加 x 除以 x。 第一步先构造函数,第二步我们直接对他使用一次拉个老日得出来他,而且我们得出来他是可塞分之一,因为 fps 导数是 s 分之一,把可塞带进去。其次不要忘了这个可塞的范围 可赛是大于一小于一加 x 的,介于它之间呢,这个东西非常非常重要,我们就是通过这个可赛的一个 大小去进行放速,而从而得到双向不等式的,所以这个可赛的放范围非常非常的关键,一定要把可赛范围写出来,那我们这一和二整个都是在对他使用拉格朗日,那我们还没有跟我们的结论去靠讨论去靠拢,那我们看我们的结论要怎么退。 已经拉格朗的形式这里已经有了,我们现在关键区把这个结论往这个拉格朗的这个形式去去靠拢,所以我们就要, 哎,因为我们要利用到拉格朗的这个结论嘛,所以都除以 x, 它这里没有 x, 所以把这个双角不等式给它除以 x, 所以第一步 a, 第一步在这里除以 x 向那个朗日的这个节能靠拢靠拢,靠拢完之后,我们我们来看一下它这一坨就是可塞分之一,所以把它变成可塞分之一大于它小于一, 然后我们要想证明这这个说明我们相当于是。呃,第一步在这里啊,我们说抑郁症,我们写一下, 欲正他就是急正他,欲正他,急正急正他。那要想正他的话,其实就是你得,因为他们都是大于零的,所以其实就是要正他大于一,小于一加 x。 哎,我发现 这个东西是成立的,所以我们再倒着写回去。哎,就可以了。所以我们整个答案的过程相当于构造了函数第一步,第二步之后,然后再倒着写回去就行了。那我们一起来看一下啊,我们把这个答案的过程给大家书写一遍。 呃,我这里写一下啊,所以我们写正令 f x 等于 long x i x 是属于一到一加 x 的,并,所以 f x 再写下,在 b 区间上面连续上连,再开向可导。我这里就省啊,再再什么什么什么可导,就把那两个条件写一下, 所以由拉式定理。因为我喜欢写拉式,就简单一点,所以由拉式定理可知。哦,你叫拉式定理?对,千万别写成拉式啊,由拉式定理可知。写一下 f 撇可塞等于 浪一加 x 减去浪一除以一加 x 减一。呃,可赛属于一到一加 x 即什么?把这个结论再写一下即可,赛分之一就等于浪,一加 x 除以 x 可 赛大于一小于一加 x。 那 ok, 好好往上挪一下啊,然后我们再继续,然后我们开始,且其实这两步都是在构造了一个函数,对,他使用了一下,拉个朗日,然后得到了这么一个结论,然后开始沿着这个箭头开始倒着写。 我们就可以说,因为可赛大于一小于一加 x, 所以可赛分之一啊,我们就可以写成大于一加 s 分之一小于。你看我都是在倒了抄啊。呃, 所以你就倒着直接倒着写就行,因为可三分之一等于他嘛,所以你落一加 s 除以 x 就大于一加 x 小于一,所以结论。呃,什么?又因为你这里可以补去,又因为 x 大于零,所以把答案抄一顿,所以这个 双向不等式两边同乘以 x 就可以了。那一加 x 小于 x, 所以正臂了,就正完了,这个正臂可以不写了, 这是完整的一个答案的一个书写的一个过程。那红色的部分是我们的分析的思路,就是你首先要去找到这个函数,然后再对这个函数使用一下,找函数,第一步,找函数,换个颜色啊,第一步,去找函数,第二步,呃,用拉,用拉式, 用拉式。第三步就是在这里开始倒推,倒推,从结论倒推, 像谁倒退就是给他整理成拉式的形式,然后开始从结论开始入手去倒退就可以了。最后写的时候是正着写的,你看我这一步都是正着写下来,正着抄下来的。 ok, 那如果听懂的话,记得给我点个赞,我们下个视频再见,记得关注哦。
303六姐讲高数 02:47查看AI文稿AI文稿
02:47查看AI文稿AI文稿同学们好,这节课给大家讲解一下倒数秒杀大招之拉格朗日终止定理的应用方法。 什么叫拉个朗日终止定理呢?就是高数当中的一个定理,我们一起来看一下。 f x 在 a b b 区间上,连续在 a b 开区间上可导至少存在一个点 x 零属于 a 到 b 的开区间,使得 f b 减 f, a 除以 b 减 a 等于 f, 一撇 x 零。 他说的意思就是在一个连续光滑的曲线上,如果有两点,他之间构成的割线的斜率,等于在这条曲线上某一点处的切线的斜率, 并且至少存在一个,比如说我上面一个是不是也是有可能的?行,那这个拉格朗日中之地,你虽然是高数的作, 但是呢,我们在高考当中应用小题来使用没有任何问题。下面我们就通过这道例题来给大家应用一下。 设 f x 等于棱眼, x 加 x 分之 m, m 属于 r, 如果对任意的 b 大于 a 大于零,有 f b 减 f, a 除以 b 减 a 小于一横乘力求 m 的范围,为什么呢? 像这种题型,其实我们有两种做法,第一种基本方法就是请听,我可以把 b 减 a 移过来,把 b 的放在一边,把 a 的放在一边,构造一个新的函数来确定它的单调性, 从而利用单调性求题目当中的参数范围。那一个是基本法,但既然说到秒杀,我们可以有更快,可能是几秒钟就可以出结果的方法,那就 是用拉格朗日终止定理。请看这个形式就吻合我们说到的拉格朗日终止定理的表示形式,也就是说,我可以得出这一块可以存在 x 零属于零到正无穷 f 一撇, x 零小于,这个地方是小于,我们在这里必须要加上一个等于一, 至于原因,这个我们到大学的时候才能给大家解释。如果你采用了这个方法,请一定记得这个地方导函数在原式基础上加上等号, 这样一来,我们利用导函数 f e p, x 零小于等于一,那我求完导,其实就可以得 x 零分之一,减去 x 零的平方分之, m 小于等于一。 在这我们来进行一个参数分离变形一下,你可以在草稿纸上算一下,很快就能出结果,是 m 大于等于四分之一。那这个就是应用拉格朗日中之定理秒杀出结果的方法。我讲完了,你听懂了吗?
1233锦源高中数学
猜你喜欢
最新视频
- 1.5万谷竹










