粉丝9137获赞3.2万
相关视频
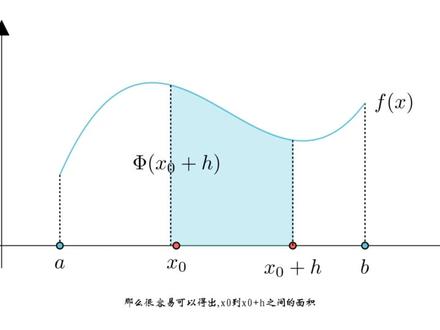 02:46查看AI文稿AI文稿
02:46查看AI文稿AI文稿第一基本定理是说,积分上线函数 five x, 它的导函数是被积函数 f x 证明,它的第一步就是将蓝色区域的面积用积分上线函数表示出来。 首先在区间 a b 内取两个点, x 零和 x 零加 h。 根据积分上限函数的定义可以知道, a 到 x 零之间的面积可以用 fi x 零表示, a 到 x 零加 h 之间的面积 可以用 five x 零加 h 表示。那么很容易可以得出, x 零到 x 零加 h 之间的面积 为 five x 零加 h 减 five x 零。这样我们就得到了这样一个等式。 下面我们为了研究积分上线函数,就需要以这块蓝色区域为桥梁,得到另一个等式。那怎么做呢? 利用积分终止定理。积分终止定理是说积分有一个上限,有一个下限, 而在区间中总存在一个点 k c, 以它的函数值为高作出矩形,它的面积在上线与下线之间,其大小与区边梯形的大小相等, 而这个红色矩形的面积等于底边 x 零加 h 减去 x 零乘以高 f k c。 然后由于它俩是相等的,因此我们得到了这样一个等式。由于这个式子的计算结果为 h, 那么整理一下就可以得到这个结果。 下面对等式两侧取极限,注意到这里是 h 区于零的极限,那么此时 x 零加 h 这个点就应该向 x 零这个点靠拢,也就是按这个方向移动。 从图像上可以看出,在此过程中, k c 也在不断向 x 零靠拢,因此左边这个式子 在求极限后就应该等于 f x 零。而对于右边这个式子,相信同学们应该一眼就能看出 它就是积分上限函数的导数定义式。通过这个式子我们可以看到 fivex 的导数是 fx, 至此我们证明出积分上限函数的导数是被积函数。
755马同学图解数学 02:38查看AI文稿AI文稿
02:38查看AI文稿AI文稿快叫你的朋友来学这个微积分入门之切值定律!作为多数高阶定律的核心之称,切值定律 可算得上是数学界的保险箱,让我们摆脱了不用算函数公式也能断定某个结果。存在的问题是微积分学习道路上的基础路标和工具,掌握它将帮你构建完整的微积分知识体系。而它的真正强大之处在于它能帮助我们减少各种复杂的计算,从而极大提高我们剪辑时间。我们先 来看一下介值定律的定义,如果一个函数 f i 克斯在 b 区间 i b 上连续,那么对于介于 f i 和 f b 之间的任何一个实数,可 a 至少存在一个点可细,使得 f 可细等于可 a。 而这里的连续则保证了函数在坐标 f i 变到 f b 的 过程中不会出现跳跃,使得中间 的每个值都会被取代。而端点值不同,则保证了函数端点值之间确实存在一个非空的中间值区间。 给你举个简单的例子,假设你徒手从海拔零米爬到海拔两千米,娜娜你的海拔高度就是一个随位置连续变化的函数,那么根据界值定律,我们能知道这里面必然存在至少一个位置,让你的海拔恰好是一千米。不用知道你具体走的哪条 路,也能确定这个位置一定存在他。在了解了这些后,我们来看看他是怎么应用的。以这道题为例,一般情况下, 我们要通过计算才能解出它的根,那也太麻烦了。可用了介值定以后,我们就不需要解除方程的根,只需要证明 它的根存在就行了。阿达降低了解析的难度,那我们就只需要设 f 艾克斯等于艾克斯的三次三加,艾克斯减一,要咒装成在区间 零一有且只有一个实根,其咒函数 f 艾克斯在区间零一有且只有一个实根。那么第一步证明函数连续,显然函数艾克斯在区间零一连续。 接着第二步计算端点值,将左右端点分别带入,从而得到这个。然后我们来到第三步,应用切值定理,因为函数 f i 克斯在 b 区间零一上连续,并且函数的端点值不同引是介于 端点值之间的数值,那么根据介值定理,总存在一点可细满足 f 可细等于零。而在这里我们就已经证明出函数 f 艾克斯至少存在一个十根。接下来只需要证明姐的唯一性就可以了。那我们继续对函数 f 艾克斯求答,从而得到这个在区间零一上到数值大于零, 所以函数 f 艾克斯在零一上单调递增,因此零点存在,而且唯一一个严格单调的函数,这都有一个零点,这求我们证明了该零点存在且唯一瞬间秒出答案。怎么样,你学会了吗?正经的知识又增加了,我是带你成长的派毛,关注我,分享更多有用知识!
7015派蒙知识 27:23
27:23 07:59
07:59
猜你喜欢
- 1817小阿文数学














