对数比大小换底公式
换底公式什么时候用?当题目中出现多个数为底,既有以二为底,又有以三为底,又以五为底,又以九为底的时候,多个底同时出现,我们就能把底统一, 咱们用到的就叫换底。换底公式说啥呢?如果现在有一个以 x 为底, y 的对数, 如果大家对这个 dx 不满意,想把它换掉,可不可以换?可以换,换成以别的数啊。以别的数,以 a 为底,这个 a 的值是多少是大家任意选择的,大家想换成谁就换成谁,但是代价是什么?最后换完他会变成一个分数, 分子,分母,它会都变成一个对数, y 放上面, x 放下边。哎,第一开始看着好像有点 复杂呢,我多举几个例子帮助大家理解一下。比如说以五为底,三的对说,哎,我不喜欢五,我喜欢什么呢?我喜欢二,我想换成以二为底,能不能可以,但是要写成分数形式,上下都是以二为底, 那真数放谁呢?三放上面,在上面呢,还放上面,在下边的还在下边,就换好了。 那有同学不喜欢二啊,有同学喜欢一百五,那我都换成以一百五为底,可不可以?当然可以,你爱换成谁换成谁,然后还是把三放在上面,把五放在下面,就这么简单。 但是通过这个例子啊,大家其实也能发现了,这个底啊,虽然是任意选择的,但是呢,不同人选的不一样,他没有一个标准,一人选一个样,那就有点乱套,这几乎没有人用,什么一百五啊,一百九,十八之类的,我们常用的是 十,为啥用十?因为我们的数都是十进制的,写成十, y 放在上面, x 放在下边,那因为呢?哎,以十为底,咱们实在是太常用的,总写 log 十 log 十太麻烦, 最为了简化,把它做一个整体,再发明一个新的符号,写成 l g。 l g 是啥意思?它表示的就是以时为底的意思, 这是我们常用的第一个数十。除此之外,我们还常用一个数,这个数字在我们学习对数之前,几乎所有的宝贝是没遇见过的。这个数叫 e, 好家伙,有点奇怪, e 不是一个字母吗?它怎么成数字了呢? 它可以联想一下,大家学习这个 pad 的时候是怎么学的呀? pad 我们知道是几来着,是三点一四一五九二六五三 等等等的一个无限不循环小数。咱不能每次写圆周率的时候都写这么一大长串,所以我们就用一个字母派来表示一个无理数,他是一个无限不循环小数。 那今天我们要学习一个新的无限不循环小数,叫一。首先这值是几呢?这值是二点七一八二八,后面的位数不用你记,但是二点七一八二八,这几位要牢牢记在心里, 大家跟我一起读,二点七一八二八,二点七一八二八,二点七一八二八,二点七一八二八,他太重要了,毫不吹牛的说,几乎各行各业,只要大家稍微接触一点高端知识, 在微积分里面,在物理学里面,在金融学里面,都有这个长数的身影,这个长数叫自然对数。一会咱们再讲讲这个 是怎么来的,以及它怎么用。咱先来用换底公式来用一下,我不写以 x 为底,我写成以 e 为底, l o g e l o g e, 把 y 放上面, x 放下边,以 e 为底。好,那因为以 e 为底太常用了,跟实是一样的, 所以我把它也起一个简单的小符号,叫 l n lion lion y b lion x, 这个 l n 指的就是以 e 为例。 那接下来我们来讲讲意到底是什么?在我们学习过程里面,我们是先学指数,再学对数,但是在真正的历史上,对数是先出现的,然后才有指数,是不是很神奇? 那?在不同的数学家研究对数的时候,甚至有的科学家在没研究对数,研究别的领域的时候,他们在 在各自的研究领域里都发现了有一个数不断的不断的出现。比如现在让大家算一个数字,一加 n 分之一,它的 n 次密,那很显然 n 代不同值的时候吧,这个整个咱算完的值,他就是不一样的 n。 如果我取一二的意思米就是二, n 取二, 一点五乘一点五就是二点二五, n 取三,我也可以算, n 取一百,我也可以算。我发现呢, 随着恩不断的在增大,这个值最后算完好像也是在增大,但是增大的有大家想象的那么快吗?我都一百次密了,按理来说什么数的什么一百次密, 给我们感觉上好像应该挺大,但是我发现这个数,即便我的恩取一万,非常非常大,他最后算出来的值其实并没有无限增长,而是一直 值。一值趋近于一个数,趋近于二点七,一八二八,我把这个值规定叫一。这个式子跟什么有关?跟银行的利率是有关的,甚至跟生物学也都是有关系的。 我们把恩取到非常非常大的时候,这个式子的值规定叫一,他是一个我们在大学阶段才会学到的一个重要极限。那有的宝宝说,哎,这式子我不懂,我看不明白,完全没关系,因为这是大学知识,大家如果有机会上上了大学,那才有可能会学到。 现在目前阶段,大家只需要知道 e 是一个数,他约等于二点七一八二八。那除了这个式子之外,有意我们在研究图形问题的时候也有意的出现。现在呢,有一个反比例函数。反比例函数大家是非常非常熟悉的,那曾经呢,有这样的一个问题, 现在我们知道一处的函数值,那很显然这段长度呢,就是一。那我把这段线段往右延展,延展成一个封闭图形,我的问题是,当他延展到多少的时候,他会使得整个延展出来这个阴影部分面积。他的面积是一类 数学家通过计算发现这个值无限趋近于二点七一八二八,实际上这玩意牛顿就会算,大家在大学学习一元函数微积分的时候,就会学到这个值也是一。 还是那句话,以上所有的有关 e 的内容,我一个字都没听懂,没关系,大家就当我在讲笑话,你只需要知道一是二点七一八二八。所以我们知道换底公式有啥用,以 x 为底外的对数,我可以换成以十为底, log y be log x 可以换成以一为底 上 line y be line x, 那究竟有啥用啊?当题目中出现多个底的时候,看有二为底就三为底,有以四为底,有以八为底,有以三为底,有以九为底的时候,太恶心,这么多底好麻烦,我直接换底 看好了。第一个数,呃,他写的是以二为底,我都换成以谁为底呢?呃,我可以换成以十为底,写成 log 九比 log 二。下面我也换,我都给他统一把底都统一成以十为底,以三为底。四对数,我写成 log 四比 log 三, 然后大家发现这九啊,四啊,都什么东西啊。九,我是不是可以写成三的平方?这帧数的头上有东西,头上的东西能怎么样来着?可以下头啊,提到前面去呗。所以本质上它其实就是二倍 log 三那类似的。四,我可以写成二的平方。 二头顶上也有东西,怎么办?赶紧下头啊,把它也放到提到前面去,写成二倍 log 二,所以最后这值是几? log 三, log 三越掉, log 二, log 二越掉,就剩一个二乘二等于四。答案选题神奇吧。 下面这题是天津卷的一道高考题,我发现底太多了啊,四八三九,看着头疼,我直接换成 统一的底,哎,刚才我是以十为底,现在我选以一为底,你选谁为底,其实都不影响最后答案。这个我写成 lion 三比 live 四,二倍 lion 三比 lion 四,加上这,我写成 lion 三比 lone 八,接下来乘以谁嘞? log 三二,我写成 log 二比 log 三,继续最后,呃, log 九二, log 二比 log 九,开始算吧。怎么化解?我发现这帧数有四, 四有八有九四,我是不是可以写成二的平方,八是二的立方,九是三的平方,所以我通通想,下头,把二下头,把三下头踢出来,把二下头 出来。那化解一下吧。这有烂呀,三比烂二,这也有烂?三比烂。二合并同类项总会吧。我只需要把这个二比二是一,一加三分之一,一加三分之一是三分之四, 所以它是三分之四倍的浪音三比浪音二乘以后面是谁,后面都是浪音二比浪音三,那前面系数,这是一,这是二分之一加二分之一是二分之三,二分之三倍的浪音二比浪音三。 那又和刚才一样,我约,我约,我约,我约,最后发现他等于二选 b, 好玩吧?做题呀,得总结呀,什么时候用换题公式 不同的同时出现,咱就大胆使用换底公式。但是我提醒大家一下,换底公式还有另外一个用处。第三种情景, 现在这个数是以 x 为底, y 的对数。刚才我是取啊,以 a 为底对不对?现在我 a 取几呢?我 a 偏偏就取 y, 我把它变成以 y 为底,可以还是不可以?只要 y 大于零且不等于一就可以呗。然后和刚才一样, y 放上面, x 放下面。 哎呦,那个歪歪,那个歪歪就是一刚讲的结论呀,分母不动,所以我惊奇的发现一个小结论,太聪明了。呃,以 x v d y 的对数和以 y 为 d, x 对数,我把真数底数如果互换位置,整个值会取到数。 这个式子的存在,它让换地公式有一个全新的用途。当大家发现一个题目里面存在一个什么对数分之一的时候,对数在分母上我非常不喜欢,我可以把真数底数调换位置,就直接写成以 b 为底, a 的对数就可以了,它能起到化碱的作用。举个例子,现在有一个二的 a, 四米是十,五的 b 四米是十。问我 a 分之一, b 分之一,他想问我 a 分之 b 分之一,我得先知道 a 和 b 分别都是几吧? a 是几二的 a 四密式时写成对数形式, a 就是以二为底十的对数,类似的, b 就是以五为底十的对数。那现在问我 a 分之一,以二为底十的对数,分之一加上以五为底十 的对数,分之一,哎,总有对数,人家还在分母上,我太头疼了,我怎么办?我赶紧把底数帧数调个个写成以十为底二的对数,加上以十为底五对数。嗯,以十为底这个写的法不标准啊,我们直接写 log 就好了。 log 二加 log 五, log 二加 log 五,同底数对数相加,帧数二和五要相乘,所以它就是 log 二乘五就是 log 十。 log 十是几呀? log 十是以十为底,以十为底十的对数,那不就是一吗?咱不是讲过以 a 为底, a 的对数总等于一吗?这个结论真的非常好用。 那还有一个常说,大家也要记下来。呃, log 一百是谁啊?以十为底十的几私密是一百嘞,十的二私密是一百, 落个一千是谁?十的几次密是一千,十的三次密是一千,所以最后答案等于一选 c。 以上我们讲了所有的公式,有纸对互换,有互逆运算,有速成运算,有加减运算。最后我们还讲了一个换底公式, 那真正的期中期末考试他怎么考?抱歉,他当然是考大综合运算了。给你个大长式子,让你在这化简。那这个式子怎么化简?我们来一起看啊。有这么多部分,那咱一点一点来呗。首先,咱从第一个开始 lion 二一方,我们知道二一方是二乘,一方帧数位帧数在相乘,我可以把它写成同底数对数的相加对不对?然后滥用二,我是没有办法化减的啊。滥用二是绝对没有办法化减的,我们这滥用一方,能不能化减一方?头上 有东西,我赶紧直接把他下头写上二倍烂亿。烂亿又是谁? line 就是以亿为例,所以以亿为底,亿的对数,那就是一呀,所以他其实是烂二 加二。紧接着我们来看第二下,这是什么东西?这里面有以三为底,有以七为底还是乘法?我们用什么公式?大家把那四个字打在屏幕上,当然我们选换底公式, 我都选以一为底啊。第一个数我写成 lion 七比 lion 三,第二个数我写成 lion 八十一比 lion 七,所以 lion 七 lion 七天然就约掉了。但是八十一我又能怎么写?八十一是九的平方,其实就是三的平方,再平方就是三的四次米,八十一写成 三的四四米,三的四四米又怎么样?头上有东西,我赶紧下头把它提出来,写成四 四倍烂三,烂三,烂三也约掉,所以最后就剩了一个光杆司令四,这是第二项的结果。第三项啊,减个烂二,减个烂二,我是没有办法花钱的哈,我就直接写了减烂二来看后面吧。这谁啊?他其实是以二为底,根号二,我能写成二的二分之一次米,对不对? 类似的,这是谁?这根号八八呢?首先是二的立方,那我根号八就相当于我在他取二分之一私密,所以他应该是二的二分之三次密啊。抄下来, 这用到什么公式了呢?有两种做法,大家可以把它看成下头公式,把它提出来,这完全没有问题对不对?我把前面抄一下啊,减烙印二这一项,烙印二,二就是一,所以我只需要减二分之一,后面一样烙印二,二是一,我只需 要减二分之三。那最后化减他浪呀二,浪呀二约掉,所以最后答案六,减二分之,减二分之三就是减二,最终答案等于四,完美。 当然我们其实还有另外一种做法,咱们再来一遍,刚才说了啊,以二为底,根和二的对数可以写成以二为底,二的二分之一,私密 咱可以用互逆运算。做吧,我现在有一个二分之一,我们对这二分之一先取指数,再取对数。你给人家两块钱,又拿走两块钱,那跟人家第一开始有啥区别呀?没有区别,就是二分之一 类似的 log 二根号八,我们刚才把它化解成为了以二为底,二的二分之三。次米,人家原来有二分之三块钱,你给了人家两块钱,又拿走两块钱,怎么办?人家还剩跟原来一样二分之三块钱,没错吧?以上就是 今天这个视频的全部内容,不用大家说,我也知道今天讲的公式非常多,而且有点杂,但是每一个公式,每一个知识点都是需要大家一定要掌握的。 所以接下来大家应该干什么?我相信不用我说,大家要做到好好做题,把今天讲这些公式,这些方法,这些技巧应用到题目当中,祝大家的对数计算学习顺顺利利,拜拜。
粉丝2.8万获赞9.1万
相关视频
 01:27查看AI文稿AI文稿
01:27查看AI文稿AI文稿咱们继续每天一道数学题看这个啊,对数运算有一个换底公式咱们都知道吧,落个 ab 就等于落个 nbb 上落个 aa。 然后呢,咱们再看一个实战一下啊,落个五四乘以,落个八五 怎么怎么办?首先是吧,换笔都换成一十位底的,可以这么写啊,就等于 log 四笔绳 log 五。然后呢,乘以呢?这边也是一样的啊,上面是 log 五笔绳 log 八, 哎,你会发现,捞个五,捞五一休,对吧,就等于捞个八分之,捞个四能看见吗?再等于啊,这下那边没地了,捞个四是 四是不是写可以写成二的平方,对吧?可以这么写啊, log 二的平方比上 log 八是不是可以写成二的三次方? 然后呢,这二呢,有一个性质,可以挪在前面来,对吧?就等于二倍的 log 二以上三倍的 烙个,这一步知道吧,烙个烙个一修就等于多少三分之二,哼,听懂了没?听懂你点个赞啊,就等于三分之二啊,这种呢,多练习就行了好。
1.3万尚钎教育 04:02查看AI文稿AI文稿
04:02查看AI文稿AI文稿换底公式的重要性无需老师多说,这是我们对数运算的重中之重,我们来看这道题啊。 呃,三的 a 次方等于四的 b 次方等于十二的 c 次方,那么 a 乘 b 乘 c 不 等于零,那么意味着是不是 a、 b、 c 都不为零,那么让我们求 a、 b、 c 和 b c。 呃,但是呢,你看,这是三个指数形式,而且呢,我们用到的 a、 b, c 都是这个指数, 那你说呢?我们要想给它表示出来呢,我们必须要进行一个只对互换,那么关键是怎么办呢?我们可以这样,哎,令三的 a 次方等于四的 b 次方等于十二的 c 次方等于 k, 是吧,那这个 k 肯定是大于零的,这是毫无疑问的。那所以根据只对互化,那么 a 就 等于以三为底 k 的 对数, b 等于以四为底 k 的 对数 c 等于。 啊哈,那怎么样啊?以十二为底,那么 k 的 对数是不是啊?啊,这个只对互化我们要先会,那么我们 abc 总算表示出来了,表示出来之后呢,我们来算 a 分 之 c 和 b 分 之 c, 所以 a 分 之 c 加 b 分 之 c, 哎,那直接给它带进去不就行了吗?那么 log 三抵 k 分 之 log 十二抵 k 加 log 币是多少啊?四底 k 分 之 log 啊,十二底 k 好, 哎呀,这些东西呢,它们的这个 底数不一样,但是真数一样,我们想要的是什么呢?底数一样我们才好判断嘛。 底数一样的话呢,那么乘变加加变成除变减减变除嘛,你只要底数一样,我们就好办。那这个该怎么办呢?其实我们用到一个非常重要的公式,哪个公式呢?我们来复习一下, 就是我们换底公式的推论, log a 抵 b 就 等于 log b 抵 a 分 之一,意思就是说呢,你交换它的底数和真数,就变成了它本身的倒数, 那么这个好办啊,那所以我们这里呢,我们给它交换一下不就完事了吗?所以你看它等于什么呀?它等于 log k 抵十二分之一,除以 log k 抵三啊,分之一, 你都把它的底数转化为 k 啊,加 log k 抵四分之一 啊,那你一除,那么就好办了,你除以它就等于乘它的倒数嘛,你除以 log k 底三分之一,就等于乘 log k 底三,所以它是 log k 底十二分之 log k 以 k 为底三的对数 加,那这个呢?还是 log 以 k 为底十二的对数分之 log 以 k 为底四的对数。 那你看到这里的话呢,我们就转化为了同分母的分数相加,哎,那同分母的分数相加, 那么最终等于 log 以 k 为底十二的对数,那么上面是呃,两个同底数相同的相加,那么相变长,所以它就是 log 以 k 为底三乘四 加变成吧。那这还不是以 log 以 k 为底十二的对数吗?那么除以它,它俩一样,那么最终结果就等于一 看懂了没有?那你看这个呢,它是利用我们换底公式的,变形公式还是非常重要的啊,所以你的换行公式呢?其实到我们高中的话呢,这个公式的运用呢,它就很灵活啊,关注老师,学习更多高中数学知识。
135许仙讲高中数学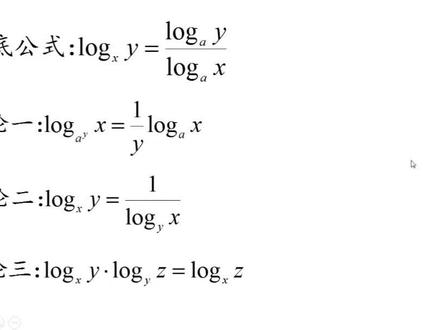 05:32查看AI文稿AI文稿
05:32查看AI文稿AI文稿同学们好,我们今天分享一下对数的换底公尺和三大推律。我们今天核心的任务就是证明一下这些换底公尺和他的三大推律。 来,咱们先看第一个换底公式,其实就是把一个对数变成两个对数相除的形式,原始对数的帧数和底数分别做分子和分母的帧数,底数给一个相同的数字就可以,但是这个数字必须要大于零,且不等于一。好,那我们接下来 按照对数换成指数的方式来做。设 log, 以 a 为底的 x 等于 m。 因为对数的含义就是帧数 x 是底数 a 的多少次,这里已经给了次数了 m 次,所以帧数 x 等于底数 a 的 m 次。同样 道理,我们设 log, 以 a 为底的 y 等于 n, 这个就能算出帧数 y 等于底数 a 的 n 次。好,这个做好之后,然后我们只要保证这个左边等于右边,就可以证明。首先是左边, 左边他是 note, 以 x 为底的 y, 我们已经算出了 x 等于什么 a 的 m 次,所以是 a 的 m 次, y 是 a 的 n 次。现在的问题就是, a 的 n 次,是 a 的 m 次的多少次, 目前还观察不出来。没关系,我们可以把这个 a 的 n 次变成 m 乘以 m 分之 n, 你看这个 m 和 m 约叫之后,是不还是 a 的 n 次。然后接下来再做闹个以 a 为底的 m, 这个可以把 m 次放在里面, m 分之 n 次放在外面,这个时候就很清楚了,帧数是底数的多少次,你看这个次数已经在这了,所以是 m 分之 n 次。然后我们再看一下右边, 右边原始是 nog, 以 a 为底的 y 除以 nog 以 a 为底的 x, nog 以 a 为底的 y 是看好啦,已经假设了是 n。 nog, 以 a 为底的 x, 已经假设了是 m。 好了,左边等于右边,已经证明。然后我们看一下推令一,推令一就是说底数上如果有个次数,这个次数的倒数就可以移到对手前面去。然后我们接下来来用换底公式来推理一下, 它是 a 的外字,这个地方是 x, 按照换底公式的意思,变成两个对数相除的形式, 原始对数的帧数和底数分别做分子和分母的帧数,然后底数只要给一个相同的数字就可以,那我们就给个 a, 这个时候你就可以看一下这个分母,分子不用变 分母这块是不应该是按照对数的含义,帧数是底数的多少次, a 的 y 次是 a 的多少次,当然就是 y 次,再一变就是 y 分之一倍的 log 以 a 为底的 x。 好了,再看一下推零二, 推零二,就是说帧数和底数如果交换位置,这两个直之间互为倒数,那我们现在看一下 not 个以 x 为底的 y, 按照换底公式,它可以变成两个对数相除的形式,原始对数的帧数和底数分别做分子 和峰里的帧数,底数给一个相同的值就可以。同样的道理, note 个以 y 为底的 x 也是一样。你看这个地方变成两个对数相除的形式, 帧数和底数分别做分子和分母的增数,给一个相同的底数就可以。这个时候你应该已经观察到他们两个之间互为倒数了。 然后我们可以乘一下 log, 以 x 为底的 y 乘以 log, 以 y 为底的 x。 然后我们可以看一下这个地方,就是 log 以 a 为底的 y, nog 以 a 为底的 x 乘以,这个地方是 nog 以 a 为底的 x 乘以 nog 以 a 为底的 y, 这个和这个约叫,这个和这个约叫,是不是等于一?所以最终就能得到他们两个 互为倒数?好,这就是推令二。然后我们最后再看一下推令三, 推六三。说两个对数相乘的时候,他们的帧数和底数是可以约分的,但必须是完全一样的数字才可以约。比如说四和四可以约,但二和六这里不能约。没有不是说约掉一个还剩一个三,这个是不可以的。然后我们接下来看 同样用话底公式 log 以 x 为底的 y 乘以 log 以 y 为底的 c, 用话底公式把它变成两个对数相除的形式, 这里的增数和底数分别做分子和分母的增数,然后底数给一个相同的值,再乘以另外一个,也变成两个对数相除的形式,这里的增数和底 数分别做分子和分母的帧数也给一个相同的底数,那这个时候他和他是不是就约掉了?约掉之后,然后我们就得到了 log 以 a 为底的 z 除以 nog 以 a 为底的 x。 这个时候你只需要把换底公式反过来用一下,是不就知道它等于 note 以 x 为底的 z。 好了,我们最后再看一眼换底公式和三大推律,祝愿每位同学都能得满分,同学们再见!
308榆次高中数学宁老师![对数比大小,这道题妙极了![高中数学] #高中数学 #高考数学 #对数 #对数函数 #数学](https://p9-pc-sign.douyinpic.com/image-cut-tos-priv/8ecc52ce5591bc1bf973681516d01975~tplv-dy-resize-origshort-autoq-75:330.jpeg?lk3s=138a59ce&x-expires=2081638800&x-signature=m%2BSdmlfjXzgcoCNKKw8tVEI19bI%3D&from=327834062&s=PackSourceEnum_AWEME_DETAIL&se=false&sc=cover&biz_tag=pcweb_cover&l=20251221090130E3C8A1E8CED32A186644) 12:25查看AI文稿AI文稿
12:25查看AI文稿AI文稿大家好,今天咱们就继续来讲一下这个对数比大小啊。昨天讲完了这个对数函数,但是比大小这一块呢,有些同学还不明白,咱来说一下。就这两道题,封面上也写了, 第一道题的话是 abc, 分别等于一个是 log 三六,一个是 log 五十,一个是 log 七十四,然后比较 abc 的大小,怎么比呢?咱们观察一下啊,你要直接画图的话,这个确实不太容易比出来,对吧?不太容易算出来, 然后怎么办呢?咱这样来,你三和六的话是什么关系?二倍的五和十又是二倍的关系,七和十四也是二倍的关系。 那索性我这个 a 的话,是不是可以把这个六写成什么形式?写成这个三乘二的形式,对吧?三乘二,这是没问题的。那看了啊,根据对数的预算法则,真数部分的乘法可以转换成对数的加法吧,相当于 log 三三, 再加上 log 三二,现在问题呢,就有了,他这个 log 三三是几啊? log 三三当然就是一了,再加上 log 三几, log 三二啊,这个没问题。 那同样的道理,既然 a 已经算出来这个结果的话, b 和 c 是不是都算出来了?那我再重新写一遍吧,扔到一块,你比较一下大小就行了。 a 是 log 三二没问题,然后 b 的话是等于一加上 log, 这个很容易啊,把十写成五乘二, 那就是 logo 二,然后 c 的话是一再加上 low 个几啊,一再加上 log 七二十四,写成七乘二就可以了,对吧? 那他比的是 abc 的大小,实际上我们分别比较的是谁的大小?只需要比较这个 a 片,然后 b 片还有 c 片, c 片的话,实际上就等于绕个圈,只需要比较这三个画圈部分 a 片 b 片 c 片的大小吧。怎么比较呢?这个咱们画图不就可以了吗?因为 a 片 b 片 c 片它三个帧数都是二,但是底数不一样, 那分别画出来啊?蓝色应该是 log 三 x 还是 log 七 x, 这个一定要注意啊,在第一线的线越远离这个外轴,它这个底数越大,所以这个蓝色的线呢?蓝色的出现实际上是 log glog 七 x, 那上面红色的话就是 log 三 x, 中间肯定是黑色的啊,是这个 log 五 x。 那画完直接以后,你看 a 片 b 片 c 片,人家自变量是 x 等于二吧,你都过一多少零画一个 x 等于二,这不就是 x 等于二,这不就画完了吗? x 等于二的话,来看了, a 片在什么位置啊? a 片他是正好等于 logo。 三二,这个不就是 a 片的高度重坐标啊,这个是 b 片,然后这就是 这片。所以说嘛,我们应该写什么?我们直接就写 a 片大于 b 片大于 c 片,实际上不就相当于你都加上一 a 大于 b 大于 c, 就整完了,对吧?这个是三个比较大小,然后拆成了这种一加上 log 三二, log 五二,然后 log 七二的形式。 但是下一个题下一个题就难了,别看起来简单啊,二三啊,行,然后 log 三四,还有 log 四五, 你说这个三十他不是大二倍啊,他绝对的差距呢,确实是三比二大了一,四比三大了一,然后五比四大了一, 参数比这样的底数呢,都大了一,但是啊,让你真正比较大,小时候直接画图,这个确实没办法,咱们还是画图啊。同样的道理,你如果画图的话,最下边就 变成了 log glog 四 x 吧,那中间这条黑线呢?就是变成 log 三 x, 最上面的话就是 log glog 二 x。 直接比较。真没办法呀,你 a 的话,咱们标一下它的高度啊,自变量是 x 等于三三的话,比如说啊,三大概在这,那这个呢?就是 a, 然后这个烙个三四的话,这个四大概。哎,四大概距离有多远?这个真不太清楚啊。不太清楚对吧?因为我们画的是草图,究竟这个四,这个位置,这个 b 和 a 究竟哪个高哪个低?肉眼看不出来,那怎么办?那没办法了,只能老老实实改一下形式了。 方法一,怎么办?跟刚才一个套路。什么套路呢?嗯,虽然哈,他的绝对差值是一,我们改成什么结果?我们能够把一个一提出来是最好的。啥意思? 这个 a 他本来是 log 二三吧,我强行在这个其中给他提出个一来。什么意思?我强行把这个三改成二乘二分之三的形式,这个是没有问题,为什么要出现二, 你知道为什么吗?好说呀,我们就是为了出现这个,你看帧数部分的乘法转换成了根据对数预算法则, low 个二,再加上 low 个二,二分之三吧,然后 low 个二实际上不就等于一?所以说同样的道理,我们还是写一遍啊, a 的话 就是一,再加上 log 二二分之三,注意二分之三是真数,那同理可得。这个 b 的话,同样的方法,我们把这个四拆成三乘三分之四,那就改成了 log 三三分之四。哦,原来是这么这么个意思哈,那继续 c 的话, 那统一可得嘛,一加上烙个四四分之五就行了。现在的话,我画圈部分,你看,我们其实只需要比较这个 a 片啊, b 片,还有 c 片的大小,就其实代表了 abc 的大小,因为他们都分别加了一,现在我们标一下 a 片, a 片的话, 二分之三,二分之三,先比较一下二分之三,三分之四和四分之五哪个大?显然二分之三大吗?人家是一点五啊,三分之四的话是一点三,三三三三循环是吧?然后呢,这个四分之五的话,那不就一点二五吗?所以这是大小关系出来了,我们先标二分之三嘛,知道这个大家的关系就行。 好,红色的二分之三最大了啊,好,这个高度呢,他就是 a 片了,那这个 b 片应该怎么标啊? b 片的话,他是跟黑线的焦点是 log 三几, log 三 x 啊, log 三三分之四,所以呢, 跟黑线的交点,这是 b 片,那继续来标吗?接下来改表什么? low 个四四分之五,那不就是最小的这个四分之五和蓝线的交点吗? low 个四四分之五,所以说这是 c 片, 现在应该懂了吧,肉眼可见的 a 片最高, b 片呢?次之啊,跟黑线焦点是 b 片,然后 c 片呢?跟蓝线焦点最低,所以就得出来什么结果。 a 片 大于谁?大于 b 片,大于 c 片,那分别加上一同样的道理,不就是 a 大于 b 大于 c 的这样一个结果吗?这个肯定是没有问题的呀。好了,我们就比完这个大小了,懂? 好吧,再说这个在告的里头就是小题的,这是方法一,画图,但是画图之前必须强行把这个一给拎出来,如果你没有做第一题的话,你觉得很容易想到这种方法吗?很不容易的,其实来看方法二。 有人说,老师我知道,我呢,可以引入一个,你看 log 二三, log 三四,然后 log 四五。那我索性索性就引入这样一个函数啊, y 等于 log x, 然后这个帧数比底数大了一个单位嘛。我引入这样一个函数, 这个函数的话,直接处理不好处理,因为帧数含有变量,底数含有变量,我们换句公式嘛,这样的话就会稍微简单一些了,换成 log x 加一,以示为底啊,底上 log x, 现在写成这个结果以后,有人说,老师,我接下来求导。别别别,因为咱现在是给高一学生讲的,咱不要讲求导的方法,咱看有没有别的方法来求。 怎么呢?其实有的看了啊,别着急,咱们慢慢来。你现在的话实际上就想比较什么。我现在其实就想证明什么呢?我就想证明这样一个很 数, y 等于 log n, n 加一,因为最小是 log 二三,其次是 log 三四,所以这个正能数 n 的话,一定记住是大于等于二的。 那写成这样一个结果的话,我想证明他这样一个函数是怎么样的?他是单调递减的这样一个函数。注意啊, y 是因变量, n 呢?是自变量,如何证明他是一个单调递减的函数呢? 好说,为了证明他是单调递减的函数,我们不就是想证明这个 log n, n 加一,减去后一项,对吧? log n 加一,然后 n 加二,怎么样啊?大于零,这不就是前头减,后边儿大于零,那不就是单调递减的意思吗? 但是变成这个结果呢?还不满意,因为你底数还有帧数都含有变量。 n, 现在的话,我们要 换底公式了啊,注意,下一步我们利用了一下什么?利用了一下换底公式,一定要回顾一下上节课的换底公式啊, 那换完底以后,索性就以十为底。刚才其实也说过了,你现在证明的是大于零嘛,实际上相当于我们把这个负的移到不能和右边去变成正的啦,相当于证明他大于他。这个其实是好说的,然后继续往后写。那继续嘛,右边的话就是 log n 加二换地公式嘛,比上烙个 n 加一, 想一想,因为你这个 n 已经大于等于二了,所以这四个画圈部分,不管分子还是分母都是正数,正数部分的话,我们直接相乘或者相处 不同的方向不变的。那接下来既然都是正数的话,我们就直接相当于证明什么?相当于证明 log n 加一改一下形式就行了,它的平方是大于 log n, 再乘烙 个 n 加二的。那如何证明这一点的?这一点的话就要需要用到什么?需要用到 y 等于 log x。 注意啊,这条图像 y 等于 log x, 它肯定是向上凸的,这个不用多解释吧啊,图像性质就是这样, 那既然如此的话,我们现在需要观察一下什么东西啊,大家现在观察这样一个不等式里头啊,最后这个不等式里头有 n, 有 n 加一,有 n 加二。首先我们就让 a 点它的横坐标等于 n 啊,注意, n 是大于等于二的,那 b 点横坐标,那就 n 加二呗。那中点的话,横坐标肯定就是 n 加一。 如果说我们先看直线啊,先不要着急,看上面这个点,先看这个直线, m 点是直线,是线段 ab 的终点啊,是 ab 的终点,那接下来怎么办呀?接下来我们根据均值不等式,均值不等式的话, a 点的 纵坐标实际上他就是什么,就是多少,就是烙个嗯,然后这个必点,这个纵坐标的话,你把这个横坐标带入,就是 n 加二吧。然后均值不等式的话,是不是大于什么东西?大于等于烙个 n, 然后再成一个 log n 加二。但是啊,我们要证明的,人家是怎么左边平方了,那就平方呗,左右两边分别平方,这样一个君子不能试改成这样一个结果,改成这个结果以后的话,我们还不满意,我们其实只需要比较一下什么,比较一下这一部分就行了。 还有一个,这个等于号什么时候取得到?等于号,只有当 x 等于外,只有当画圈部分这两项相等的时候,画圈部分这两项能相等吗?不可能,所以这个等于号其实是永远取不到等于号,只能取这样一个大于号。别着急,别着急,你着什么急? 我们其实已经可以说几乎已经出来这个答案了,看了啊,同学们,我们来看这个恩典坐标是什么东西啊?显然这个恩典坐标我们可以写成 log n 加一,这是恩典的纵坐标吧, n 点纵坐标,它是大于什么的? n 点纵坐标,它是大于这个 m 点的纵坐标的,这个 m 点纵坐标我们根据终点公式其实已经写出来了,它就是二分之 y a 加 y b, y a 就是烙个 n, y b 就是烙个 n 加二,懂了吧?所以说接下来 log n 加一的平方是不是大于这样一个二分之? log n 加上 log n 加二,这是终点公式,对吧?这样一个整体的平方呢?大于这个整体的平方,那就大于 后边这一项。那我们圈一这个不等式不就证明完了吗?圈一证明完了,因为我们每一步都是等价变化过来的,所以说最终就证明了原来他是一个减函数。现在呢?你可以截图了,因为我要擦掉这一部分了啊。 也就是说最终我们证明了原来 y 等于 log n, n 加一,它是一个减函数。那既然是减函数的话,你看这个二三四,虽然越来越大了这个 n, 但是整体却越来越小了。因为是减函数,所以就是 log 二三反而大于 log 三四。 唠个三四反而大于唠个四五,这不就写完了吗?这是方法二。那如果让你选择的话,你会用哪种方法比较大小呢?分享课堂知识,感受数学之美。我是杨范老师,下期课再见!
3.2万会放羊的教书匠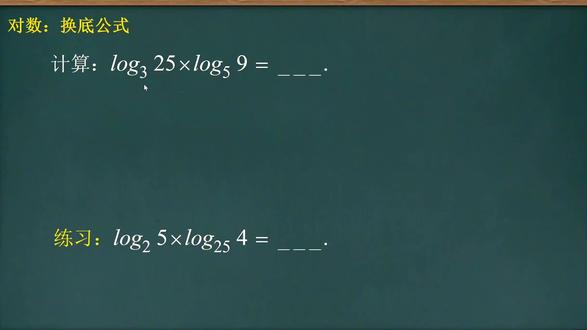 00:53查看AI文稿AI文稿
00:53查看AI文稿AI文稿这种对数连成,我们用换底公式教大家如何来描。首先我们前面这个对数,我们可以写成 log 除以 log, 然后差一个增数,记住上面这一个在上面,下面这个在下面,同理这一个来跟着做一下,首先 log 除以 log, 然后上面这个九在上面,下面这个五在下面,然后你看约不了怎么办?我们要改一下,把这个二十五,二十五写成五的平方, 五的平方,然后这个二可以拿到外面来,所以这就没了啊。然后洛克五是不是就可以跟这个洛克五约掉了? 就是分子乘个二,然后九可以,因为这里是三,把九写成三的平方,然后这个平方来到外面来啊,变成二倍的洛克三,这个平方没了,然后洛克三和洛克三是不是约掉了?你看就剩两个分子的话,二和二分母是一乘一,所以说二得四秒了,你听懂了吗?这一个动手练一练吧。
846小郑老师讲数学 05:15查看AI文稿AI文稿
05:15查看AI文稿AI文稿对数运算换底公式不会用,我今天教你不用公式怎么算,现在我有一个小小的要求, 给我学会,再点赞,不用换底公式,把这些题都做出来。第一题你说太简单了,口算都出来了,是不是二乘二得四?好, 那第二题呢,你还能口算出来吗?不太能了吧,但是我能是吧。三为什么很简单啊?这个四和这个四怎么着能够消掉,就变成 log 二八, 也就是解,也就是三,原理就是什么呢? log ab 乘以 log bc 等于 log a, c 就是 这两个 b, 怎么着,只要一样一上一下就干嘛消掉?那你看第三题,是不是这个二和这个二怎么着消掉,变成什么 log 三三, log 三三是几,是不是一呀? 懂了吗?能做所有的乘法题啊,然后再来。哎,你知道第四个怎么 不一样了是不是?那怎么办呢?那咱就给它变一变啊,在对数当中呢,只要这个数能写成几的几次方,就给它写一下,你看 log 三八就可以写成什么 log 三,然后呢?八写成二的三次方, 这个三呢,是可以往前提的啊,就变成三倍的 log 三二, 那下一个呢?落个四九,我就可以写成什么啊?这个四变成二的二次方,这个三呢?变成三的二次方,这个二往前提变成分子,也就是和这个三一样啊,也就是二倍的。 那这这个二呢?要干嘛?变成分母,也就是二分之二。注意了啊,上面这个数往前提 变成分子,下面这个数变成什么分母?二除以二,是不是一啊?所以就变成这个东西啊,就变成 log 二三了, 最后就变成什么三。 log 三二乘以 log 二三等于几啊?等于三,为什么?这俩玩意一一乘是不是变成一了?剩个三能跟上吗? 第五题怎么做呀?你看啊,这个 log 二二十五,我是不是写着什么 log 二五,是不是五的平方呀?我直接怎么着往前写乘以什么呀?这时候我已经看见了啊,看着 log 三二 二能跟上吗?为什么?因为四,我要写成二的二次方,再乘以什么 log 五三二, 然后啊,你看啊,我先把这些数都乘一块,二二二是不是得八呀? log 二五 乘以 log 五三,就变成 log 二三,因为五五怎么着消掉,那 log 二三再乘以 log 什么三二是不是一呀?最后答 八。那你看第六题啊,第六题毁了,是不是出什么了?出这个分母了。那怎么办呢? 一除以 log 三二十一,就会写成 log 二十一三, 老师,为什么呀?就因为这,你看他俩相乘是几是一,这叫什么?互为倒数,也就是 log 二十一三加上 log 二十一七, 这怎么用啊?这个有一个公式叫做里积外合,你现在不会也没关系啊,以后我会讲到里积外合。什么意思啊?现在?现在是合给它变成里边变成积二十一,三七,二十一等于一, 就这样直接去倒数就行了。那第七题怎么做? log 三四乘以 log 四八乘以 log 八 m。 你 说老师我已经都会了啊,四四怎么着消掉乘 log 三八八,再怎么着消掉 log 三 m, 等于 log 三分之一七。那接下来怎么做呢?它是不是这是三呀?这是什么?三分之一我就给它变一下,我给它写成什么 log 三的负一次方,然后七,这个负一是不能往前提。当然了啊,记着一提变成什么? 变成分母负一分之一,是不是还是负一?所以这个啊,注意了这个式子,这有点乱了,就写成负的 log 三七,但是还没有完呢啊,他说 log 三 m 等于什么?我再把这个负一啊, 摆到这个什么七上边,就变成 log 三七的负一次方是七分之一,所以 log 三 m 等于 log 三七分之一, m 等于多少 七分之一。记着啊,这个方法所有的乘法都能用,这只是换底公式的一个。嗯,叫什么变换,讲完你听懂了吗?
691单招数学邪修 02:14查看AI文稿AI文稿
02:14查看AI文稿AI文稿单招数学对数换底公式,轻松拿捏单招数学常考的换底公式题型,一招带你快速搞定!当考试遇到这种底数不同的一个对数时,怎么计算呢?这时候我们就要用到换底公式了, log 以 a 为底, b 的对数,其中 a 的话是底数, b 的话是帧数,我们都换成 log 以 c 为底的一个对数。那换底的时候呢?我们这个 b 的话,帧数跑到分子的位置,底数 a 跑到分母的一个位置,最终的话也就写成了 log 以 以 c 为底, b 的对数除以 log 以 c 为底, a 的对数。通常的话,我们 c 的话,为了方便计算,取可以取十。 log 以以 c 为底, x 的对数就变成 log 以以十为 为底, x 的对数,那 log 与十啊,就是那个 a 开始,那这个时候我们的原式就变成 log 以 a 为底, b 的对数等于那个 b 除以那个 a。 ok, 那我们来看这道题目, log 以八为底,九的对数乘以 log 以二十七为底,三十二的对数。这个设置呢,我们可以运用换底公司进行一个化减,也就是那个九除以 那个八,乘以那个三十二除以那个二十七。其中我们九的话就可以写成三的平方,八的话,我们可以写成二的三次方。 二十二,三十二,三十二的话,我们可以写成二的五次方,二的七,我们可以写成三的三次方。 根据对数的一个运算性质,这个帧数部分的咪可以放在前面当一个系数,那我们这个狮子也就化减成二,那个三除以 三六个二乘以五,六个二除以三六个三, 那我们这个设置一销,这个设置一销,最终的结果的话,就等于三分之二乘以三分之五等于九分之十,你听懂了吗?记得点赞关注哦!
673良辰老师讲升学 18:52查看AI文稿AI文稿
18:52查看AI文稿AI文稿同学们好,我是董老师,今天我们继续来讲对数的换底公式。我们昨天已经讲了对数的三个运算性质,若 a 大于零,且 a 不等于 m, n 大于零的情况下,那么对数会将 乘法运算变为两个同底的加法运算,除法运算就变回变成两个同底的减法运算,乘法运算就变成一个乘法运算。注意,那这里面只有同底的对数相加减 才可以合并起来,否则的话,不同底的必须先变为同底才可以合并起来。那我们继续回顾对数的概念。我们在对数的概念里面,我们知道,若 a 的 x 方等于 b, 其中 a 大于零, a 不等于一, b 大于零,那根据对数的概念,我们可以得到 x 是等于 log ab。 对于等式, a 的 x 方等于 b。 我们假如在等号的两边取以 c 为底的对数,那么我们会有什么呢?我们这边看一下 两边求与 c 为底的对数,左边是 lock c a 的 x 方,右边是 lock c b。 根据我们昨天的一个运算性质,左边 指数 x, 它是可以提出来的,因此正面会变成 x。 log c a 等于 log c b, 这里面我们可以将 x 解出来,就会得到 x 是等于 log c b 除以 log c a。 又因为前面是等于 log a b, 因此我们可以得到一个 横等式,那这个式子就叫做换点公式。换点公式 log a, b 等于 log c b 除以 log c a。 其中 a, c 都是大于零, a, c 都是大于零,而且 a c 不为一。为什么呢?因为我们这里面底数要大于零且不为一,帧数, b 是要大于零的啊。特别的,当令上数的式子中的 c 等于 b 的时候,那我们就会有什么呢? 左边 log a b 不动分子式 log c, 分子式 log b b, 因此分子是一, 而分母是 log b a, 因此我们就可以得到 log a, b 是等于一除以 log b a。 当然也得保证底数 b 是大于零且不为一的。类比下列 分数的变形,我们发现左边是一个分数变分母,而右边是一个对数换底。这两者之间他们都有相同的逻辑啊,是有一个欲取同工之妙。 那换底公式它的作用是什么呢?一般的科学计算器,我们通常只能用常用对数或自然对数进行计算,若是要计算 log 二三,我们该如何计算呢?这里面我们就可以利用到换底公式。 对于 log 二三,我们可以把它改成以十为底的常用对数,所以它是等于 log 三除以 log 二,而 log 三利用计算器算出来是约等于零点四七七一。 log 二是零点三零一零,因此相足会约等于一点五 五八五零。我们知道,一般的或者说以前数学家他并不会将所有的对数表列出来,一般只会选取一些常用的对数或自然对数进行列表。 可能一些以二为底的对数或以三为底或以五为底的对数,他可能列表列不出来,或者有很多。那此时利用换底公式,就可以将之化为我们很常见的一个或者以十为底或以自然底数一为底的一个常用对数 方法。我们正面是以十为底,也可以将之化化为以一为底的自然对数。 log 二三,它可以等于是 roin 三除以 roin 二, roin 三约等于一点零九八六, roin 二约等于零点六九三一,因此这个还是约等于一点五八五零。 那换底公式就是涉及到这里面的一个这样的用处。好,我们来计算下面三个题,我们来先来看第一个, 这里面是哪里计算? log 九八乘以 log 三十二二十七。那这种计算该如何处理呢?我们可以这么来处理, 正面,我们将里面的底数,因为正面有底是九,还有三煞,我们将将其通通化为以十为底的,或者说以一为底的。我们这里面以十为底的对数运算。 所以第一个圆式,它是等于是 log 八除以 log 九乘以 log 二十七 除以 log 三十二。然后利用我们昨天所学的一个运算的性质, log 八是等于三倍的 log 二, log 二是七是等于三倍的 log 三分母, log 九是等于两倍的 log 三, log 三十二是等于五倍的 log 二。 这是利用到我们昨天所学的性质,将乘方变为一个乘法运算啊。那你现在就会发现,落个二,落个三正好全部消掉,分子是九,分母是十,因此此题是等于十分之九,这是第一个, 第二个我们也是同理的,我们可以将之全部化为以十为底的常用对数,那么我们可以得到,这是 log 二十五除以 log 二乘以 log 四除以 log 三乘以 log 九除以 log 五进行变形。 log 二十五可以改写成是等于两倍的 log 五 拿来, log 四是等于两倍的 log 四, log 九是等于两倍的 log 三除以 log 二, 所以 log 三,所以 log 五。你会发现 log 二, log 三, log 五正好跟分母相消,所以这个圆式是等二乘以二乘以二是等于八的, 这是前面两个换底公式的运算,我们就是第三个。这里面我们也可以通通化成以十为底的常用倍数,那么元数就等于 log 二十五,我们前面写了 log 二十五是等于两倍的 log 五除以 log 高。第二个是指是 log 二根号二除以 log 三,后面一个 log 五九就是等于 log 九除以 log 五。 好,我们整理一下,分子是等于两倍的 log 五乘以 log 二根号二啊,这里面是 log 二根号二,根号是二的二分之三次方,所以是二分之三。 log 二。 log 九是等于二乘以 log 三, 然后跟分母相消,是 log 二。 log 三。 log 五正好只留下了一个二乘以二分之三乘以二,因此得到的结果是为六。 这是第一个计算问题,可以先把它画成同底的对数,再进行运算。我们再来看一个 变式,第一个圆式正面是两倍的 log 根号二, log 根号在里面是相当于 二分之一的意思,因此咱们稍微可以改一下,就是两倍的正面是二分之一。 vlog 二 括号的平方加上后面 log 根号,又有 log 根号,所以是二分之一。 log 二乘以 log 五, 后面是一个根号,后面这个正好是一个完全平方公式,他是正好等于根号 log 根号二减去一括号的平方, 这个根式里面不大好,不大好。注意到那同学们可以稍微验证一下我这 logo 根号二减一或者平方是不是正好等于正面的啊?或者你把这 logo 根号二的平方拆开来, 你会发现它是等于四分之一。 log 二括号的平方减去 log 二加一,所以它正好是等于二分之一。 log 减一括号的平方跟里面的式的是一样的, 那后面我们整理一下,前面是二乘以四分之一,那就是二分之一 log 二括号的平方加上二分之一 log 二 乘以 log 五加上正面是一个完全平方,那此时我们可以开根号开出来啊,正好就是一减二分之一 log 二啊。那么咱们进行整理一下, 这里面我们全部对这几个式子,我们全部可以提个二分之一 log 二出来,因此它会等于二分之一。 log 二括号正面 是 log 二,加上 log 五减去一,剩下一个一是单独写在旁边这个括号里面。 log 二加 log 五正好是 log 十是等一,一减一正好是等于零,因此正面是零加一正好是等于一。这是第一个变试题, 我们继续看第二个。第二个 log 五百 log 五百加上 log 五分之八,减去二分之一 log 六十四,这里面都是同底的对数的运算,因此咱们可以先利用性质把它写成 log 括号五百 加就变成乘乘以五分之八,好,减就变成除除以。这里面二分之一是不能单独提出来的,二分之一应该先放到里面去,六十四的二分之一是方,那正好是 八,因此要除以八加上五十,后面是一个平方,而 log 二加 log 五,其实正好是等一,直接加五十即可,因此它是等于 log 正面五百乘以五分之一,正好是 log 一百加上五十,而 log 一百是等于二,因此它是等于五十二。第二个比较简单,前面是一个计算问题,我们继续看这里面的求职问题, 他说已经知道 log 七三等于 a, log 七四等于 b, 用 ab 来表示 log 四十九四十八, 前面是给出以七为底的对数,后面居然是以四十九为底的对数,因此咱们也可以把这个 log 四十九四十八改成以七为底的对数运算。所以点 log 四十九四十八改成以七为例,那就是等于 log 七四十八除以 log 七四十九。 对于分母来说,四十九正好是七的平方,因此是等于二分之一。 log 七四十八,那 log 七四十八我们又可以怎么办呢?这里面四十八其实是可以写成四的平方乘以三的,因此它又会等于二分之一。 log 七四的平方乘以三,因此它是等于二分之一 log 七四的平方加上 log 七三。整理一下,正面就是相当于二分之一括号两倍的 log 七四加上 log 七三啊,因此它是等于二分之一括号 log 七四是等于 b, 因此是二 b 加上后面是 a 啊,这里面就是二分之 a 加二 b, 因此 not 四十九四十八,它是二分之 a 加二 b。 我们可以利用 a 来 a 和 b 来表示这个数值。 第三,用换底公式证明以下两个很等式,一个 log a 的 m 次方, b 的 n 次方是等于 m 分之 n log a b。 那此时我们可以将这个通通化成以 a 为底的对数,将左边划就行了,左边推到右边,因此左边是等于 log a b 的 m 字, b 的 n 次方除以 log a a 的 m 次方。因此证明,对于分子来说,利用我们昨天的学的性质,三可以得到是 n log a b, 而分母正好是 m, 因此它是等于 m 分之 n log a b 即为所求 是第一个换题公式。第一个公式其实以后我们在解题里面也是可以使用的,而且使用的频率还比较高。 第二个我们也可以正面是证明很等式,三个正好都是不同底的,我们可以把它先变为同底。所以第二个左边就等于 log b, 所以 log a 乘以 log b, c 呢,就是 log c, 所以 log b。 然后呢, log c, a 呢,就是 log a 除以 log c。 而发现 log a 正好,分子也有,分母也有,也抵消了 b, log b 也是一样的, log c 也是一样的,因此全部相销正好是的一,因此第三个用换底公式来证明这两个式子是特别方便的。 那第三个其实在几个对数相乘底数之间是可以相互转化位置,帧数之间也可以互换位置的,同学们可以记住这个定理,以后在解题里面也是可以直接使用的。四个求职与证明, 已知 x y z 为正数,且三的 x 方等于四的 y 方等于六的 z 方等于 m。 第一问,求 on x 除以 y 的值, 我们使用它的时候,我们无非就是将 x 解出来,可即可。好,正面将 x 解出来,我们相当于指数或对数,因此 写 x 可以写成是多少呢? x 是等于 log 三 m, 同理 y 是等于 log 四 m, 这个呢,是等于 log 六 m。 好,那正面要求二 x 除以 y, 二 x 除以外,带路过去就是两倍的 vlog 三 m 除以 vlog 四 m。 啊,那这里面我们通通化成以十为例,定常用对数,那这里面就是两倍的 vlog m 除以 vlog 三, 三除以 log m 除以 log 四。而这里面你会发现 log m 正好是相消,转化一下,它就是等于两倍的 log 四除以 log 三。 整理一下,它是等于多少呢? log 四又可以写成是两倍的 log 二,因此它是四倍的 log 二,所以 log 三, 然后再进行化解,这里面可以写成是 log 三二,四倍的 log 三二,因此这里面它的答案就是等于四倍的 log 三二。 这个是需要注意的,换底之后还得换回来,我们继续看第二个,第二个他让你求证这个横等式,其实证明这个横等式也是比较简 简单的,我们可以利用前面的解除 s y z 带入过去就行了。那一除以二万,我们就可以得到。是等于一除以两倍的 log 四 m 一岁, z 是等于一岁。 log 六 m 一除以 x 是等于一除以 logo 三 m, 其实正面通通可以转化一下, 对,一除以二 y, 我们可以知道它是等于两倍的 log 四 m, 那等于多少呢?正好是等于二分之一。 log m 四, 这里面无二 y 分之一还可以稍微化解,它是等于 nog m 二,因为四是可以写成二的平方,平方 二放到前面去,跟二分之一正好抵消。好,这是二 y 分之一,那这一分之一,那我们就可以改写成是 log m 六。 x 分之一,它就是等于 log m 三, 此时你带路过去,所以 log m 二正好是等于一,所以 z, 那就是 log m 六。减去 log m 三, 正好符合我们昨天学的一个同底的对数相减,底数不变,增数相除, 因此它正好是等于 log m 二。那圆不等式,那圆等式我们就可以得正,所以二 y 分之一是等于 z 分之一,减去 x 分之一。那第二个它的证明是 思想,我这里面是相当于把 y z x 先求出来,然后利用换底公式,我们可以得到二 y 分之一,它是等于 log m 二 z 分之一是 log m 六, x 分之一是 log m 三,此时就化为同底,我们就很好判断他们之间是否相等了。 好,那么我们进行一个课堂小结。本节课学的是一个换底公式,正面 log ab 等于 log cb 除以 log ca, 特别的时候,当 c 等于 b 的时候, log ab 是等于一,除以 logba, 正好跟分数换分母是他们的原理是一致的。 当然这里面还有一个变式,你们说这两个式子,同学们以后大家也是可以记住的。对于第一个来说,这 a m 次方,如果他的次数占 底数上,那么我们就应该放在分母,如果这个指数指数密是在帧数的上面,那么我们就放在分子。 第二个式子,我们前面说过几个对数相乘,不管是同底还是不同底,他们的底数之间是可以互换位置,帧数之间也是可以互换位置的,这个需要同学们记住。好,本节课学习的就是一个换底公式,希望对大家有所帮助。
1000咚铛铛 06:04
06:04
猜你喜欢
- 1503二年级张老师

![对数的换底公式[高中数学] #换底公式 #高考数学 #对数 #高中数学 #对数函数](https://p9-pc-sign.douyinpic.com/image-cut-tos-priv/f969e22ca73d56639d9e87b751175915~tplv-dy-resize-origshort-autoq-75:330.jpeg?lk3s=138a59ce&x-expires=2081638800&x-signature=oNmZrugwnC70%2FX1lxWM9ldfR8PM%3D&from=327834062&s=PackSourceEnum_AWEME_DETAIL&se=false&sc=cover&biz_tag=pcweb_cover&l=20251221090130E3C8A1E8CED32A186644)







