九上数学圆的14种辅助线做法
粉丝176.0万获赞1776.1万
相关视频
 00:33查看AI文稿AI文稿
00:33查看AI文稿AI文稿九、上数学最难的圆的十四种辅助线,全部背熟,稳进班级前三。九上数学常考圆的十四种辅助线做法,一、遇到弦时。二、遇到九十度圆周角时。三、遇到有直径时。四、遇到弦时。五、遇到有切线时。六、遇到证明某一直线是圆的切线时。 七、遇到两香蕉切线时,切线长。八、遇到三角形的内切圆时。九、遇到三角形的外接圆时。十、遇到两圆外离时。十。一、遇到两圆的香蕉时。十。二、遇到两圆相切时。十。三、遇到三个圆两两外切时。完整可分享!
68古德猫宁 00:35查看AI文稿AI文稿
00:35查看AI文稿AI文稿九、上数学最难的圆十四种辅助线,三天吃透,稳进班级前三。九上数学常考圆的十四种辅助线做法,一、遇到弦时二、遇到九十度的圆周角时。三、遇到有直径时四、遇到弦时五、遇到有切线时六、遇到证明某一直线是圆的切线时 七、遇到两相交切线时八、遇到三角形内切圆时九、遇到三角形外接圆时十、遇到两圆外离时十一、遇到两圆相交时十二、遇到两圆相切时十三、遇到三个圆两两外切时十四、完整可分享!
 00:33查看AI文稿AI文稿
00:33查看AI文稿AI文稿九、上数学最难的圆的常用辅助线全部背熟,逆袭班级前三圆常用辅助线添加技巧,一、连半径构造圆心角。二、构造同弧或等弧所对的圆周角。三、构造圆内接四边形。 四、构造直径所对的圆周角。五、与垂镜定力有关的辅助线。六、与切线有关的辅助线。 八、辅助员九中考切线真体辅助线完整电子版留分享!
34懒惰小美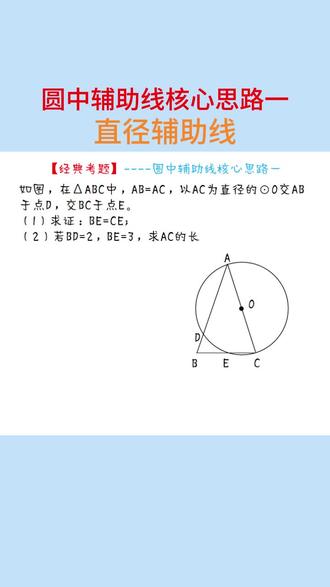 02:27查看AI文稿AI文稿
02:27查看AI文稿AI文稿圆中的辅轴线你知道要如何去做吗?在圆中的几何题,如果给出直径,那么我们能够利用的就只有直径所对圆周角是直角, 而直角不仅是特殊角度,还能够带来特殊三角形。因此,有直径造直角 方式呢,也就是连接直径另一端点与圆周上的点了。先从索求逆向思维分析,想要证明 b、 e 等于 c、 e, 就 优先将目光放在 b、 e 与 c、 e 所在位置, 此时结合已知条件中的 a、 b 等于 a、 c, 不 难发现三角形 a、 b、 c 为等腰三角形,而 b、 c 为等腰三角形的底边。那么想要证明所求,就要从等腰三角形底边三线合一入手, 那么就考虑连接 a、 e 来证明 a、 e 与 b、 c 垂直即可。对于圆来说,仅仅给出直径 a、 c 就 让我们想到直径所对圆周角是直角,那么证明 a、 e 与 b、 c 垂直也就没有什么难度了。 对于第二个问,想要求解 a、 c 的 长,绝大多数求解线段都是要利用直角三角形的, 而 a、 c 为圆的直径。对于直径,我们所学内容只有直径所对圆周角是直角这一个几何理论 已经连接了 a、 e 能够得到直角三角形 a、 e、 c, 又考虑能否利用已知条件求解所求,倘若不能,就需要再次构造出新的直角三角形。 很明显,已知条件仅能让我们求出 c、 e 而无法求出 a、 e, 那 么就不能利用直角三角形 a、 e、 c 来求解所求。自然想到连接 c、 d 构造新的直角三角形, 不仅可以利用已知条件求出 c、 d, 同时可在直角三角形 a、 d、 c 中利用勾股定律列方程求解 a、 c, 此时设 a、 c 的 长,并且表示出 a、 d 的 长,即可。利用直角三角形 a、 d、 c 以及勾股定律来得到方程求出所求圆中直径辅助线的思路,你学会了吗?
26小乔伊 00:39查看AI文稿AI文稿
00:39查看AI文稿AI文稿九上数学最难的圆的辅助线做法,全部背熟,考试稳上九十八家!九上数学常考圆的十四种辅助线做法,遇到弦时,解决有关弦的问题时,遇到九十度圆。九长时, 遇到弦时,遇到有切线时, 遇到三角形的内切圆时,遇到两圆相交时。以上内容均有完整版。
17吃葡萄不吐皮🅿 00:29查看AI文稿AI文稿
00:29查看AI文稿AI文稿九上数学圆的十四种辅助线全部背熟,逆袭班级前三!九上数学常考圆的十四种辅助线做法,一遇到弦时。二、遇到九十度的圆周角时。三遇到有切线时。 七遇到两相交切线时。八遇到三角形的外接圆,十一遇到两圆相交时。完整版分享!
192小葫芦🌞 00:39查看AI文稿AI文稿
00:39查看AI文稿AI文稿九上数学最难的圆的辅助线,三天吃透开学领跑全班!九上数学重点压轴圆的常用辅助线类型一,圆半径构造圆心角类型二,构造同弧或等弧所对的圆周角类型三,构造圆内接四边形 类型四,构造直径所对的圆周角类型五,与垂镜定力有关的辅助线 类型六,与切线有关的辅助线类型七,内切圆与外接圆常用的辅助线类型八,辅助圆类型九,中考切线真体辅助线有完整电子版可分享回。
28李李爱分享 00:37查看AI文稿AI文稿
00:37查看AI文稿AI文稿九上数学最难的圆的辅助线,三天吃透开学领跑全班!九上数学重点压轴圆的常用辅助线类型一,圆半径构造圆心角类型二,构造同弧或等弧所对的圆周角类型三,构造圆内接四边形 类型四,构造直径所对的圆周角类型五,与垂镜定力有关的辅助线 类型六,与切线有关的辅助线类型七,内切圆与外切圆常用的辅助线类型八,辅助圆类型九,中考切线真体辅助线有完整电子版可分享回。











