log2X=3公式
粉丝15.1万获赞222.9万
相关视频
 02:24查看AI文稿AI文稿
02:24查看AI文稿AI文稿对数运算,当然我们最喜欢的是底数,相同的对数,一看这个底数好像有那么点关系,都跟二有关,于是咱们就动点小心思,把它变一变。熟悉的同学就看得出来这是二的平方,那么就联想到当年这个公式, 这个公式说的是底数的指数可以放到前面来做系数的分母,而增数的指数可以放到前面来做系数的分子。 应用这个公式,这块就会变成这个二还是这个二。底数的指数放前面来做分母,那是二。真数的指数是一啊,放前面来做分子,那是一,于是就会变成了这个样子,放在前面一算,就变成一了,于是他就得出了这个结果。 同样道理,这个八呀,怎么看出它是二的三次方,于是按照这个公式一写,底数的指数出来做系数,分母,真数的指数是一啊,出来做分子,于是就变成了这个样子, 前面这个括号呢,就简化成了这个样子的,那加起来不就是三分之四吗?所以就是三分之四倍的二为底的上涨对数。如果这个公式你不熟悉呢,你完全也可以直接运用换底公式,你把这个东西啊,直接换底, 变成以二为底的对数,或者你直接换成以十为底也行,怎么方便就怎么来。来看第二个括号,这个数已经最减了,没法化减,找超的呗。 这个底数是九,那就三点平方,那按照这个公式来写,这个指数出来是分母,那是二分之一, 两者加起来,那显然是二分之三,以三为底的幺的对数,这两个数要相乘,数跟数乘,剩下二,这个对数跟这个对数、底数增数位置对调,那恰好就是一用的是这个公式嘛, 它依然也是由换底公式推导出来的,相乘等于一,于是最后结果就是二 选项就有了。回顾一下这个问题,就告诉我们,当底数真数啊,它数比较大,特别是恰好是一些数的完全平方的时候,我们可以利用这些公式把它先化简化,简完以后再来计算。
![对数+指数分段函数,零点个数问题这么解才快 今天给大家讲解一道经典的高中数学分段函数零点问题,已知f(x)=\begin{cases}|\log_2x|,x>0 \\3^x,x\leq0\end{cases},函数g(x)=[f(x)]^2-2(m+2)f(x)+4m恰有5个零点,求实数m的取值范围。视频里会拆解f(x)的图像特征、换元法转化方程、根据零点个数分析参数范围,一步步带你理清解题思路,高中数学遇到同类题再也不怕啦!有疑问的同学评论区留言,我会一一解答~
#高中数学 #分段函数 #函数零点 #参数取值范围 #高考数学](https://p3-pc-sign.douyinpic.com/tos-cn-i-0629/owxwrAA1pBACgReHCwFEgKD8nRAVAwAIE7fpC8~tplv-dy-resize-origshort-autoq-75:330.jpeg?lk3s=138a59ce&x-expires=2081808000&x-signature=FXssvkIhYvqP11umuHjgTV9pTng%3D&from=327834062&s=PackSourceEnum_AWEME_DETAIL&se=false&sc=cover&biz_tag=pcweb_cover&l=20251223083511CF9B761C1BEB0535D587) 04:27查看AI文稿AI文稿
04:27查看AI文稿AI文稿分段函数与二次函数相结合,求零点的个数,这类题型难倒了大批学生,我们看一下本题他的一个突破点,核心考点在什么地方, 也就是先画出 f x 的 图像,那我们第一步画出 f x 的 图像,由于它的图像是分段函数,所以我们在这要划两部分,这不妨是一小于等于零的时候是一个指数函数, 三到 x 侧方,然后大于零的时候是个对数加绝对值。所以此时我们把它的图像这样画出来,就像这么走的一个图像,我们这就是 f x 的 一个图像, 我们看一下它,这里告诉了恰好有五个零点,我们在这里串圆,令 f x 等于 t。 大家想一下这个 t 是 代表啥?代表的是 f x 的 值域, 它的值域的情况。所以换元之后,我们不妨令 h t 就 等于 t 方减去二倍 m 加二倍 t, 再加四 m, 这个方程刚好要等于零时,恰好有五个根, 那我们想一下,要满足有五个根,他这判别式一定是存在的。等于零时只有一个根,那很显然与这交不可能交五个交点,那说明这一定是判别式是大于零,一定存在有 t e t 二两个根的关系。既然是两个根的关系,我们看一下图,第一种情况下,这一条线与它相交,这是 y 等于 t 一。 第二种情况下,这是 y 等于 t 二。大家数一下,这的交点个数恰好有五个,满足条件,所以此时我们在这里的话,就会得到判别式单调, 使 b 方减去四 a c 四倍 m 加二的平方减去四 a c 十六 m 大 于零,这是第一个方程 而存在。你看这一个根是零到一之间,这一个根是大于一的,那我们可以想象成二次函数的一个图像。二次函数这个根, 这儿是零,这儿是一,所以这儿是 t 一, 这儿是 t 二。那我只需要满足的是 h t 零一定是大于零, h 一 一定是小于零。把这个零代入之后,这儿得到四 m 是大于零的这一根儿,把一带进去,这儿是一,减去二倍, m 加二,再加上四, m 是 大于零。 我们可以根据这里把它解出来之后,是由于 m 是 大于零这两个数连的这连的之后,就可以得到零小于 m 小 于二分之三,这是它的一个解集。但是还有一种情况, 当它的根刚好恰好有一个根,等于另外的一个根,是有三个焦点,这种是 y 等于 t 二刚好等于一的时候,等于一的时候,这儿刚好是另外的一个根,是 y 等于 t 一。 它 t 一 是属于零到一之间时,此时 我们利用两数之和可以代替两数之和, t 一 加一等于两倍, m 加二, 然后 t 一 乘以 t 二等于四, m 把 t 二换成一,代替那 t 一。 我们这儿解出来之后, m 这个数刚好等于二分之三。所以这两种并上之后,就是我们的中上,就可以选出答案是 b 项,它可以取到二分之三。
 00:38查看AI文稿AI文稿
00:38查看AI文稿AI文稿高中数学对数式大公式,吃透它,孩子对数题再也不用愁!对数加法、对数减法、对数乘、对数连乘 换底公式互为倒数,只对互化两个特殊值,两个转换。 重要推论,关注我,帮您图解数学!
35刘老师奥秘数学 05:28查看AI文稿AI文稿
05:28查看AI文稿AI文稿现在相当多的相机都支持各种 log 的 灰片拍摄了,但是说实话,现在能把 log 拍明白的人说实话也不算多。许多人拍完 log 素材回家一还原,要么就是画面黢黑或者说噪点爆炸,然后丢下一句 log 真难用,然后就去拍普通素材了。用拍照片的思路来拍摄 log 素材的视频,出现这个情况真的不算奇怪。 log 绘片并不是一种滤镜,而是一种为了在有限的数据量下榨出更多动态范围和画质的记录策略。如果你想让你的视频拍摄只敢提升一个档次的话,那么就继续往下看吧。 再一开始,我们有必要说明为什么我们的拍摄视频的时候需要使用 log 直接拍不行吗?这就不得不说到我们的相机传感器和我们人眼一个相当大区别的部分了。对相机而言,接收到的亮度是二,输出的也就是二。 但是对于人眼来说,就以这幅图为例,你看后一个方块的亮度,是不是感觉是前一个方块的亮度的基础上加了百分之十, 但是实际上我们看到的这个图后一个方块的亮度其实是前一个的一倍。这在科学上已经证实,人类对于光线强度的感受和非人类的仪器测量的实际强度的值是以对数为正比的。所以说我们可以发现,像是快门速度 每调亮一档,实际上的曝光时间就是增加一倍。这意味着我们人眼实际上对微弱光线的改变感受更为敏感,而对于更大亮度的改变其实没有那么敏感, 但是相机对光线的记录则是限性的,接受的光线亮度翻倍,电信告也翻倍。如果这样直接记录下来信号,我们可以发现一个令人震惊的事实,就是大部分数据都用来存储高光部分的数据了,甚至像是最亮的一档就占据了百分之五十的数据量, 这显然是不合理的。然后另外一方面的话,由于我们的显示器并不能百分之百还原我们现实中全部的亮度范围,所以说为了保证显示器显示的画面看起来更加正常, 我们会在拍摄的时候使用 rock 七零九的色彩空间,通过压缩部分高光数据所使的观感更加接近人眼直接观看的感受。在 rock 七零九的曲线下,我们就能看到高光下的数据得到了压缩,从而增加了暗部的数据量。 当然了,实际上亮部仍然是占据了大部分的数据量的,那我们是不是就可以更进一步,进一步的压缩高光部分的数据量?毕竟我们人眼对于高光的敏感程度远远没有暗光部分敏感, 于是我们就看到了相机上的各种 logo 曲线,我们在 logo 曲线下就会发现每一档之间的数据量分布就会更加均匀,这样我们能记录下的动态范围就要更大。不过这样拍摄出来的画面就会丢失掉大多数的对比度,画面看起来就是一片灰色, 这样会导致我们在实际拍摄过程中很难直接通过画面来确定和色曝光,这就是很多人在拍摄过程中翻测的最大原因。 你说直接用 lot 还原预览来参考曝光可以吗?其实那也不太可以,比如说我们在拍摄过程中直接参考 lot 还原的预览,调整到和色曝光的话, 我们再用监视器的波形工具来看 log 下的波形图,我们会发现它的波形其实也就占据了全部的一半左右,这就相当于浪费了差不多一半的数据量, 所以说噪点多也就不难理解了。要减少噪点,提升画质,充分利用 logo 带来的优势的话,我们就要想办法让曝光在不溢出的情况下尽可能的更多。 不过我们在这里有一个前提,那么便是增加曝光的手段,可以是降低快门速度,可以是增大光圈,也可以是增加灯光,唯独不是提升感光度。道理很简单,增加 so 只是简单的把相机信号获取放大,并没有增加我们相机接收的光线数量。 感光度只需要在原生的感光度之间调整就可以了。比如说 h s 三,在光线足够的情况下就用六百四的低档原声 s o, 暗光下的话就直接用一万两千八的第二档原声 s o。 那 我们要怎么确定曝光尽可能高的情况下又不过曝呢?最简单的方式就是使用斑马线,不 过需要注意的是,不同 log 曲线的高光截止点是不一样的,比如说所谓大多数相机的 log 三在百分之九十五亮度的地方截止, 比如说索尼,在 s l o 三下就可以将斑马线设置为百分之九十五,而佳能在用 c l o 二的时候设置成百分之百就可以了,保证画面主体不大量出现斑马线的情况下,就可以认为曝光是合适的。 至于灯管、金属、高光之类的部分,你就让它出现斑马显示,让它过曝也无所谓。但是如果你把斑马线设置的比 log 曲线截止点还要高的话,就会出现画面已经过曝了,但是完全没有斑马线提示情况 或者设置过低的话,就会出现无法完全利用整个相机画质的情况。当然对比较专业的拍摄的话,我们还会使用监视器来做拍摄的时候的辅助监看,借助波形图来确定更加合摄曝光, 可以直观的看到画面各处的曝光情况,让波形尽可能在填满的时候避免高光的波形在顶端消平,这样一来我们就能充分榨干画面的效果,尤其是对于半画幅的相机来说,画面的噪点就能得到一个很好的改善。但这样拍摄出来的画面,如果你直接在后期套用官方 logo 还原的话, 有很大可能直接给你一个过波的画面。但是你不要着急,我们只需要你保证在前期拍的情况下没有出现斑马线或者说波形消平的情况,就说明这个画面其实是没有丢失数据的,只需要将曝光拉回,我们都能找回到它的全部细节。 而且比起直接参考 note 预览来曝光的情况下,有着更少的噪点和更多的动态范围。当然我们在后期还原的时候,选择正确的色彩空间以及对应的还原 note 也是非常重要的。 关于如何正确的使用降低了 log 灰片模式,我们今天就给大家分享到这里,这里是大川为你分享生意干货,如果这视频对你有帮助的话,欢迎点赞、关注、转发给你需要的朋友,我们下期再见,拜拜!
1650索之巅 大川同学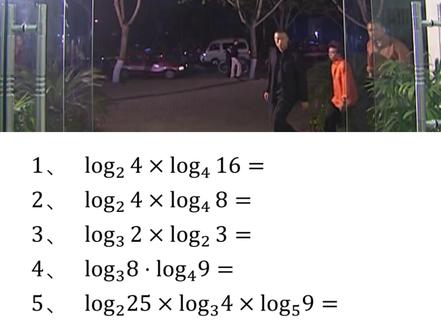 05:15查看AI文稿AI文稿
05:15查看AI文稿AI文稿对数运算换底公式不会用,我今天教你不用公式怎么算,现在我有一个小小的要求, 给我学会,再点赞,不用换底公式,把这些题都做出来。第一题你说太简单了,口算都出来了,是不是二乘二得四?好, 那第二题呢,你还能口算出来吗?不太能了吧,但是我能是吧。三为什么很简单啊?这个四和这个四怎么着能够消掉,就变成 log 二八, 也就是解,也就是三,原理就是什么呢? log ab 乘以 log bc 等于 log a, c 就是 这两个 b, 怎么着,只要一样一上一下就干嘛消掉?那你看第三题,是不是这个二和这个二怎么着消掉,变成什么 log 三三, log 三三是几,是不是一呀? 懂了吗?能做所有的乘法题啊,然后再来。哎,你知道第四个怎么 不一样了是不是?那怎么办呢?那咱就给它变一变啊,在对数当中呢,只要这个数能写成几的几次方,就给它写一下,你看 log 三八就可以写成什么 log 三,然后呢?八写成二的三次方, 这个三呢,是可以往前提的啊,就变成三倍的 log 三二, 那下一个呢?落个四九,我就可以写成什么啊?这个四变成二的二次方,这个三呢?变成三的二次方,这个二往前提变成分子,也就是和这个三一样啊,也就是二倍的。 那这这个二呢?要干嘛?变成分母,也就是二分之二。注意了啊,上面这个数往前提 变成分子,下面这个数变成什么分母?二除以二,是不是一啊?所以就变成这个东西啊,就变成 log 二三了, 最后就变成什么三。 log 三二乘以 log 二三等于几啊?等于三,为什么?这俩玩意一一乘是不是变成一了?剩个三能跟上吗? 第五题怎么做呀?你看啊,这个 log 二二十五,我是不是写着什么 log 二五,是不是五的平方呀?我直接怎么着往前写乘以什么呀?这时候我已经看见了啊,看着 log 三二 二能跟上吗?为什么?因为四,我要写成二的二次方,再乘以什么 log 五三二, 然后啊,你看啊,我先把这些数都乘一块,二二二是不是得八呀? log 二五 乘以 log 五三,就变成 log 二三,因为五五怎么着消掉,那 log 二三再乘以 log 什么三二是不是一呀?最后答 八。那你看第六题啊,第六题毁了,是不是出什么了?出这个分母了。那怎么办呢? 一除以 log 三二十一,就会写成 log 二十一三, 老师,为什么呀?就因为这,你看他俩相乘是几是一,这叫什么?互为倒数,也就是 log 二十一三加上 log 二十一七, 这怎么用啊?这个有一个公式叫做里积外合,你现在不会也没关系啊,以后我会讲到里积外合。什么意思啊?现在?现在是合给它变成里边变成积二十一,三七,二十一等于一, 就这样直接去倒数就行了。那第七题怎么做? log 三四乘以 log 四八乘以 log 八 m。 你 说老师我已经都会了啊,四四怎么着消掉乘 log 三八八,再怎么着消掉 log 三 m, 等于 log 三分之一七。那接下来怎么做呢?它是不是这是三呀?这是什么?三分之一我就给它变一下,我给它写成什么 log 三的负一次方,然后七,这个负一是不能往前提。当然了啊,记着一提变成什么? 变成分母负一分之一,是不是还是负一?所以这个啊,注意了这个式子,这有点乱了,就写成负的 log 三七,但是还没有完呢啊,他说 log 三 m 等于什么?我再把这个负一啊, 摆到这个什么七上边,就变成 log 三七的负一次方是七分之一,所以 log 三 m 等于 log 三七分之一, m 等于多少 七分之一。记着啊,这个方法所有的乘法都能用,这只是换底公式的一个。嗯,叫什么变换,讲完你听懂了吗?
741单招数学邪修 00:24
00:24 02:29查看AI文稿AI文稿
02:29查看AI文稿AI文稿啊,同学们,我们看一下啊,我们上一个视频讲的是说底数和真数永远差的是同一个数,那我们这个视频看一下啊,这个底数是三,真数是九,它的底数是四,真数是十二,那它不是相差的是同一个数,而这里边真数永远是底数的 三倍啊,你看十二是四的三倍,九是不是三的三倍?所以相当于我们构造一个函数是 log 以 x 为底 三, x 是 不是这个对数啊?那么我们现在看一下啊,这里其实啊,它可以真数的乘法,它可以写成两个同底的数的加法计算,所以它可以写成的是以 x 为底三的对数,再加一, 那我们现在看比较它的大小,是不是比较前者的大小关系?那我们现在看一下啊,说以三为底九的对数,它可以写成以三为底,那么三乘以三,那所以说一 再加上的是 log 以三为底三的对数,那这个很明显它就是得几啊二,而那我们接着看一下,以四为底四乘以三, 那它可以写成一加上是不是以四为底三的对数啊?以四为底三的对数,它比一小,所以一加上比一小的数,是不是一定比二要小?那也就是说我们能得到这里以四为底十二的对数,它小于以三为底九的对数。 好了,那么接着同学们看啊,我利用的是对数同底的加减运算的逆运算,给它写成 log 以 s 为底三的对数,再加一, 那么其实它等价于就是如果 f s 等于以 x 为底 k x 的 对数,那么如果在这里边它的 x 大 于一, k 大 于一时,其实它同样也是一个单调递减函数, 它可以写成以 s 为底, k 的 对数再加一,那么我们借助于对数的这个图像,你看啊,比一大,那如果你 k 比一大时,是不相当于在这儿,而我们它的上边的图像,它的底儿要 小,下边的图像是不是底要大?所以底越小的,它的函数值是不是越在上方?那么这个值是不就越大?所以我们看 x 越小,它整体的值是不是就是对应的越大啊?只根据这样一个函数,它的单调性横是一个单调递减的啊。
19徐思数学 04:08查看AI文稿AI文稿
04:08查看AI文稿AI文稿在对数的运算中啊,这个换底公式呢,我们必须要牢牢地掌握住,而且要灵活运用。你看这道题呢,就是一道难题,已知 log 三比二等于 a, 三的 b 次方等于五,则 log 以十五为底, 根号下三十的对数,用 a b 表示为多少?好,那么这里的话呢,大家你想一想啊,你要想用 a b 来表示,你得知道 a b 是 谁呢? 你看啊,我们这里的 a 等于 log 三点二,我们已经有了,那么三的 b, 四方等于五,我们可以得出这个 b 等于几呢,知道不?知道呀,那么只对互化,那么就是以三为叠 五的对数,说白了哈,我们就是要把以十五为底,根号下三十的对数转化为谁呢? log 三抵二和 log 什么呀?就是你转化到 ab 身上嘛, 和 log 三抵五身上去,对不对?就是要把它转化到他俩身上,那么如何转化他俩身上呢?你看他俩的底数都是几? 他俩的底数 a 与 b 的 底数都是三,而这个呢,底数是十五,那我们就可以怎么样了,用换底公式了。那么换底公式怎么写的?我这里给你写一下。 log a 抵 b 等于 log c 抵 b, 比上 log c 抵 a, 那么这个 c 只要大于零且不等于一就可以。那么你说我们在对它进行换底的过程中,我们选谁作为新的底,你选谁都可以, 只要大于零不等于一,是不是就行了呀?那么你看 ab 的 底数都是三,所以我们这个 c 是 不是应该选择三呀? 那么其他的你就不要再选了。哎,这是很自然而然,那么这种思路是很丝滑的啊,很丝滑的,那么所以他就等于以三为底,根号下三十的对数, 他是呢?以三为底,十五的对数,反正你这个真数要与二和五取得联系, 那怎么取得联系?呃,非常简单,那么你看啊,他等于谁? log 这个根号下三十,呃,相当于是三十的二分之一次方,这个二分之一我们可以给他提到前面去,三抵三十比上 log 三抵十五。好,那么这个二分之一我们给它提取到前面去,上面的三十我们可以分解成什么呢?反正我们分解出来的要有二和五, 那就什么呀?二乘五乘三,这是三十,那么下面呢?十五 是三乘五有三我们不怕,因为你底数是三嘛。好,那么乘变加,那不就是二分之一倍的 log 三抵二加 log 三抵五加 log 三抵三, 比上下面乘变加 log 三抵三加 log 三抵五。好,给它带进去,等于二分之一乘 a 分 母 log 三抵二是 a, log 三抵五是 b, a 加 b, 然后呢?呃,这个 log 三抵三是一,然后下面呢? log 三抵三是一,一加 log 三抵五, log 三抵五是 b, 对吧?那所以等于二倍的一加 b 分 之 a 加 b 加一。那么这道题我们就做完了,是不是用 a 与 b 来表示这样的一个式子?所以我们这道题的最终结果呢,就是二倍的一加 b 分 之 a 加 b 加一。啊,就这样写就可以了哈。呃,这是我们换底公式的灵活运用。哎,非常非常重要,也是我们期末考试的重中之重,关注老师学习更多数学知识。
161许仙讲高中数学 03:43查看AI文稿AI文稿
03:43查看AI文稿AI文稿黑板上的这道题呢,百分之八十的同学呢,期中考试的时候都没有做出来啊,为什么呢?呃,因为他只会死记硬算啊,你看啊,前面这个括号里边有三项,后边这个括号里边也有三项, 那如果我要是用多项式乘对式,我给他展开的话,那是不是要有九个式子呀?那你还不一定能算出来,而且非常容易出错。这道题呢,我们就需要先观察,先别忙着算对不对?你看啊,他的底数是二四八, 真数的一百二十五,二十五五,那么二四八有什么特征呢?二的一次方,二的平方,二的三次方,一百二十五,二十五五呢?五的三次方,五的平方,五的一次方。那么后边这个呢,底数是五二十五,一百二十五,真数是二四八。 那么其实在这里边的话呢,我们就可以怎么样啊?利用我们换底公式或者换底公式的推论,先进行一个转化。怎么转化来,先喊他声姐, 对吧?原式等。哎,这个步骤你太会啊,所以第一个呢,它第一个括号里面 log, 二底五的三次方加 log, 你 看啊,这个四是多少呢?是二的平方,五的平方。 哎,这个真数是五的平方加 log, 这是二的三次方和五,这个五呢,你可以看成五的一次方, 然后乘 log 五抵二加 log, 那 么二十五呢?是五的平方,四十二的平方,这个一百二十五是谁呢?是五的三字方,八呢是二的三字方。哎,这个能看懂吧, 对不对啊?那你看,都转化为二和五乘上去了哈,你看前面这个是多少呢?三倍的 log, 二抵五加,呃,这是二分之二,你提到前面去, 这个公式会不会 a 的 m 次方的 b 的 n 次方的对数,那么是不是就等于 m 分 之 n log a 抵 b 啊, 对不对?那你二分之二倍的 log 二点五,所以这是一倍的 log 二点五,然后加三,这可以看成五的一次方,那就是三分之一倍的 log 二点五。反正我们第一个括号里面全都转化成了 log 二点五啊。后边 啊,一样的 log 五抵二加,这是二,二分之二是一,那么 log 五抵二,再加三分之三是一,那么一倍的 log 五抵二。哈,你看这两个括号其实都是同内向,也类比着这个意思啊,那我们就可以给它合并哈。 三加一,再加三分之一,那就是三分之十三倍的 log 二抵五乘啊。后边是三倍的 log 五抵二,那么三分之三分之十三乘三,那就是十三倍的 log 二抵五乘 log 五抵二。嗯,那这个公式该咋算呢?那么大家记不记得我们的换底公式还有一个推论叫做什么呀? log a 抵 b 乘 log b 抵 a 等于一, 他俩互为倒数,对吧?所以我们这个 log 五抵二乘 log 二抵五就等于一,所以他的最终结果就是十三。哎,这道题你学会了没有?呃,你要是没学会的话呢?前面我们换底公式的几个推论一定要给他姥姥掌握住啊,关注老师,学习更多高中数学知识!
154许仙讲高中数学









