几何体内切圆半径
粉丝34.6万获赞116.7万
相关视频
 00:19查看AI文稿AI文稿
00:19查看AI文稿AI文稿treat treat! treat treat。
2975同学请看题|初中数学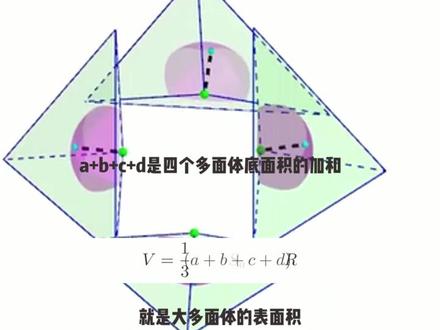 01:10
01:10 02:56
02:56 02:42查看AI文稿AI文稿
02:42查看AI文稿AI文稿圆柱棱柱内切球高与半径手牵手之前的视频我们连续讲了空间几何体的外接球问题,从今天开始,我们介绍另一个题型,几何体的内切球。 首先大家要知道,并不是所有的几何体都有内切球。先用圆柱举例,如果一个圆柱存在内切球,由于上下底面均与球相切,那么圆柱的母线长就等于球了直径,并且底面圆的半径恰好等于球的半径。 这样我们就得到了圆柱存在内切球的条件以及内切球半径公式,大二等于小二等于二分之 l, 这里的大二代表圆柱内切球半径,小二代表圆柱底面圆半径。而对于一个直棱柱,同样可以适用这组公式。由于直棱柱 上下底面与球相切,所以直棱柱的高就等于内切球的直径。我们在观察俯视图,此时内切球的图像恰好变为与底面多边形各条边都相切的内切圆,并且内切圆的半径就等于球的半径, 那么我们就得到相同的公式,大二等于二,内等于二分之 h, 这里的二内代表底面多边形内切圆的半径。最后我们做两道题,熟悉一下公式, 圆柱内有一个球,该球与圆柱的上下底面及母线之相切,那么该球为圆柱的那些球 满足。公式,大二等于小二等于二分之 l, 圆柱的体积 v 等于派二方,乘以 l, 利用等式将小二和 l 转化成大二,则二派二的立方等于十六, 所以派二的地方等于八派,再将八派带到球的体积公式中,得到微球等于三分之三。十二派。 第二题,一个球与三龙柱的三个侧面、两个底面都相切,则该球为龙柱的内切球。利用球的体积公式 v 等于三分之四拍二的立方得到内切球的半径大二等于二。 再根据大二等于二,内等于二分之 h 得到高 h 等于四底面内切圆的半径二,内等于二。 由于正三棱柱的底面为等边三角形,根据图像我们可以发现, ap 的长恰好等于内切圆的半径 op 长的根号三倍,所以我们得到公式二分之 a 等于根号三倍的二内,所以 a 等于四倍。根号三。三棱柱底面正 三角形的面积 s 等于四分之根号三倍的一方,结果为十二倍。根号三,三棱柱的体积 v 等于 sh。 最终结果四十八倍根号三,你们学会了没?
519高中数学曹师傅 05:00查看AI文稿AI文稿
05:00查看AI文稿AI文稿大家好,我们一起来看一下这道题。今天呢,我们要推导一下直角三角形内切圆拌进了这个公式,其中二级三角形 abc 中角稀释九十度, 然后呢, ab 分别表示是直角边,这个 c 呢是表示的斜边, r 表示的是内屈原的半径,那么最后这个内屈原呢,他会等于二分之 a 加 b 减 c, 也就是二分之直角边的和减去斜边。好,我们写一下推倒过程证明。 首先我们要从已知条件出发,就是说在 rt 三角形 ab 西中,我们要把脚西等于九十度的条件抄下来,这样才能说明大西 小西,小西是鞋边。好,接下来呢,我们从和入手呢,我们从这个三角形 abc 的面积入手, 那我们观察图形哈,这个辅助线的做法已经给出大家了,我们连接 o a oboc 以后呢,整个三角形 abc 的面积就可以切割成就是三角形呃, aoc 的面积加上 boc 的面积加上 aob 的面积,那也就是二分之一 a, 什么二 加上二分之一闭眼,再加上二分之一吸眼,那么这个简单的过程我们不去推倒了,就把它拿过来直接用了哈,那最后呢,就是二分之周长乘以内前半径, 然后直角三角形直角边互为底和高,还可以写成二分之直角编织机。那么这样呢,我们首先就 推导出这个内气源的半径,它是等于 ab 哈,除以这个 a 加 b 加,行,那我们来观察一下啊,这个结果和我们要求证的结果哈,还差的好远呢,怎么办呢?那我们就联想到直角三角形三边关系定理,什么叫直角三角形三边关系定理, 我们脑子要灵活一点啊,我这样说就是勾股定理,西方等于 a 方加 b 方。接下来也是这道题的难点,我们要利用完全平方公式的一个公式,变形,把平方和写成和的平方减去二 ab, 好,这个时候我们来观察一下哈,就是 a 加 b 跨平减二, b 等于谁啊?等于西方。那么这个时候呢, 我们就能够表示出哈,我们上面这个不是有个 ab 吗?我现在把它表示一下啊, ab 等于什么呢?仔细观察一下这些符号啊,他就等于,呃, a 加 b 块平方减去西方除以二。好了,这样呢,我们把它带入到我们上面那个推倒结果里面啊,这二他等于什么了呢?呃,就把那个 ab 啊,呃,下面这个 a 加 b 加西不动。 然后呢,就是把那个 ab 等于二分之 a 加 b 块外平方减西方,我们给它抄起来 好了,那么接下来我们怎么推倒呢?接下来我们上面这不是平方差吗?只需要音式分解 就可以了,利用平方差公式好,把前面括 a 加 b 看上一个整体,减去 c 的平方两数和乘以两数差。那我们分解的结果呢?就是 a 加 b, 嗯,加西,然后乘以 a 加 b 减西。好了,我们这个结果终于马上要出来了哈,我们看看最后什么结果呢? a 加 b 加西约掉了 啊,越掉了。那我们最后的结果呢,就是等于二分之 a 加 b 减膝内切圆半径等于二分之 a 加 b 减膝二分之直角边的和减去斜边。好了,我们整个就推倒好了,我们回个头来小结一下啊。首先我们第一步我们采用的是面积法,就是列了一个等式, 表示出这个三边和内全半径的关系。那么虽然,那我说这个怎么不就是直接就应用他当 公式了,哎,其实当用它当公式好像也可以,但是呢,我们还有更简单的公式啊,更简单的公式,这里面就运用了一个勾股定理哈,勾股定理以及完全平方公式的一个公式变形哈, 这里我就不写了。那么接下来到最后一步,我们如何化解呢?临时分解 也是分解,所以我们这道公式推倒下来哈,因死记硬背没有用,记不住。推倒下来的话,要求呢我,我们还要有一定的基本功啊,有一定的解题经验才可以。好,本题就讲解到这里,下次再见。
690马老师初中数学 04:43查看AI文稿AI文稿
04:43查看AI文稿AI文稿最近后台有好几个粉丝私信我,问我三角形内千元的半径如何去求?今天我们通过一个例题来详细讲解 说三角形 a、 b、 c 为直角,三角形 a、 b 等于四十厘米, b、 c 等于四十二厘米, a、 c 等于五十八厘米。求应用部分的面积。哎呀呀,求应用部分的面积啊,那我们就要求出圆的面积就可以了。三角形是一个直角,三角形那高和低我们都知道,所以三角形的面积可以求出来, 用三角形的面积减去里面,这个圆的面积就是硬部分的面积。那要想求圆的面积,咱们就要知道圆的半径,那圆的半径如何去求呢?这里面就牵扯到了小学阶段一个重要的公式,内千元半径公式 为,二等于二 s 除以 c, 这里的 s 是三角形的面积, c 是三角形的周长。那 这个公式如何推倒的呢?我们具体来看,三角形 a、 b、 c 内切一个圆,已知三角形的面积为 s, a、 b 等于 a, b、 c 等于 b, a、 c 等于 c。 求圆的半径,分别过这三个切点,做三条垂直于三角形三条边的垂直线, 这时候这三条垂直线相交于 o 点,那这个 o 点其实就是圆的圆心,那这三条垂直线就是圆的半径。好,我们设为小二, 然后再连接 a、 o、 b、 o 还有 c、 o, 如图所示。那从图中我们可以发现,三角形 a、 b、 c 的面积被分成了三份,一份是 三角形 a、 o、 b 的面积,一份是三角形 b、 o、 c 的面积,还有一份就是三角形 a、 o、 c 的面积。所以 s 三角形 a、 b、 c 就等于 s 三角形 a、 o、 b 加上 s 三角形 b、 o、 c 再加上 s 三角形 a、 o、 c, 这三个面积之和, 又已知这三条线段分别垂直于三角形 a、 b、 c 的三条边,所以分别就是三角形 a、 o、 b、 b、 o、 c、 a、 o、 c 的高高呢,都是圆的半径二,所以三角形 a、 o、 b 的面积就等于 底。是 a、 b 等于 a 乘二除以二,那三角形 b、 o、 c 的面积就是它的底, b、 c 是等于 b 乘二除以二。同理,三角形 a、 o、 c 的面积就是底, a、 c 是等于 c 乘二除以二,它们加起来是等于这个三角形 a、 b、 c 的面积。好等式的。两边同时乘以二,也就是阿尔斯等于 a 二 加上 b 二,再加上 c 二好。这个等式,它也等于 a 加 b 加 c 乘以二, 那二就等于二。思除以 a 加 b 加 c 好。 a 加 b 加 c 是三角形 abc 的周长,我们用大写的 c 来表示, 由此可以推导出内切圆的半径二就等于二四除以 c 好。知道了这一公式,我们回归本题。二等于 二十除以 c, 我们给它带入的公式中,那三角形 a、 b、 c, 它的面积就等于四十乘四十二除以二,等于八百四十平方厘米。 那三角形 abc, 他的周长就是四十加四十二,再加上五十八,等于一百四十厘米,所以圆的半径就是二乘八百四,再除以一百四等于十二厘米,所以圆的面积 就等于派二的平方,也就等于三点一四乘以一百四十四,算出来的结果是四百五十二点一六平方厘米好。阴影部分的面积,它就等于三角形的面积 是八百四十,减去这个圆的面积四百五十二点一六,算出来的结果是三百八十七点八四平方厘米。其实直角三角形属于特殊三角形内尖圆半径。有个更简单的公式 是二等于 a 加 b 减 c 除以二,也就是两个直角边的和减去斜边的长再除以二。但是这个公式推导运用到了初中的传统三角形的知识,这里就不过多表述了。关注我,带你学习更多的数学知识!
1834张老师数学思维 02:14查看AI文稿AI文稿
02:14查看AI文稿AI文稿三角形的内切圆半径公式是怎样表示的呢?这里有一个任意的三角形 abc, 他的三条边分别是 abc, 我们现在做出他的内切圆圆欧,那么圆欧的半径应该如何用他的三条边 abc 来表示呢? 我们首先做出他的半径,我们连接圆心和三个切点,根据圆切线的性质,其实这三条线是和三角形的三条边是垂直的,而且这三条线就是那切圆的半径,我们用而来表示。 我们再连接三角形的三个顶点和圆心,就把这个大三角形 abc 分成了三个小三角形。通过观察我们发现大三角形 a, abc 的面积其实就是等于这三个三角形的面积。我们来看一下这个紫色的三角形,紫色的三角形的面积是啊,二分之一 a 乘 l, 绿色三角形的面积是二分之一, b 乘 l, 橙色三角形的面积是二分之一 c 乘二,那么这样我们就可以把三角形 abc 的面积表示成二分之一, a 乘二,加上二分之一, b 乘二,再加上二分之一, c 乘二。 我们通过整理就可以得到三角形的面积等于二分之一 r 再乘 a 加 b 加 c, 然后我们就可以表示出 r 等于 a 加 b 加 c, 分之二 s, 注意这个 s 就是三角形 abc 面积。那有些同学又会产生疑问,那这个面积如何用三条边来表示呢?我们就要用到海伦公式, 海伦公式是这样的,三角形的面积等于根号下 p 乘 p 减 a, 再乘 p 减 b, 再乘 p 减 c, 这个 p 啊就是半周长,也就是 a 加 b 加 c, 再除以二, 这样我们通过这两个公式就可以用三角形的三条边来表示他内切圆的半径。
1278潘小童讲数学 02:26
02:26 01:52查看AI文稿AI文稿
01:52查看AI文稿AI文稿原来内切球半径这样子解真的很简单。大家好,欢迎来到李老师数学思维课程,今天我将用类比的思维方式教大家如何快速求解 内切球问题。我们来看一下这这一种类型题求三棱锥和四棱锥的内切球。很多同学在这种立体图形的一个模型构造里面呢,他会陷入一个瓶颈,他的思维里面无法构造出这样的立体图,从而导致 这种类型题的内切求的半径求不出来。那么今天李老师教大家用类比的思想快速求解这类型的题目。 我们以三棱锥为例,我们把三棱锥类比成为我们的一个三角形的内切圆的问题,那么这道题就会变得非常容易。 我们来看一下这个三角形里面有个内切圆,我们通过等面积法 把这一个三角形的一个未切圆的半径给它求解出来。大家看一下这个三角形的面积,我们可以用 b、 c 层高哈求出来,然后我们也可以把它切成三份, 三份去求解它的一个面积的表达形式,那么这一块我们就可以把这个 are 给它求解出来了啊。 那么在这一块里面,当我们遇到三轮锥的一个题目求那些球的时候,我们就沿用我们平面所学的知识点,进行等体积法的一种类比思想,等体积法 去把这一个三棱锥的体积分成四份,那么这道题就会变得非常容易。关注我李老师口诀,带你轻松快乐学数学!
134李老师数学思维 01:32查看AI文稿AI文稿
01:32查看AI文稿AI文稿中考必刷题!在一个直角三角形中,要证明内切圆的半径等于两条直角,边的和与斜边的差等一半。那我们怎么证明呢?这个圆哦,是直角三角形 a c, b 的内切圆。首先我们假设三个切点分别为得一 f, 那我们看到的圆心 看到了切线,就马上会想到连接圆心和切点构造直角,所以我连接欧德 o e 和 o f, 它会产生三个直角原外一点像圆影,两条切线的长度相等,所以我们得到第二个等量关系,就是 b, e 等于 b f a, f 等于 a do, 并且 do c 等于 c。 假设这个圆的半径为啊这个四边形 o do, c 一有三个直角,并且两个零边 分别相等,它一定是一个正方形。就知道 c 得边等于 c, 边要等于 r。 假设角 a 的对边为小 a, 角 b 的对边为 小 b, 角 c 的对面为小 c, b, f 等于 b, b 是等于 a 减去 rbf 也等于 a 减去 raf 等于 a 等于 b 减去 r。 我们知道 af 加 fb 等于 c, 那么这个时候就可以得到三条边与 r 的关系了。因为 b 减 r 加上 a 减 r 要等于斜边 c, 所以 r 等于二分之, a 加 b 减 c。 关注火山哥数学,拿满分!
 00:19查看AI文稿AI文稿
00:19查看AI文稿AI文稿不要惊讶,你知道吗?所有的圆锥有内切球的棱锥棱抬,他们的体积除以表面积再乘以三,就是内切球的半径了。球体的内切球就是他自己,所以球的半径、体积和表面积也满足这个关系时。
1.9万数学高分老曹 01:00查看AI文稿AI文稿
01:00查看AI文稿AI文稿通通秒杀,什么叫做极致的效率问题呢?像这种椎体内切球的题目,你只需要做这一道题,那么其他的题目呢?和这道是完全一样的,根本不需要做别的题目,不需要什么题。海战术。你, 你看啊,只要是椎体的内切球的问题,你通通带入这个公式,就可以计算出这个椎体内切球的半径。 记清楚啦,锥体体内最大的球就是内切球,一切的锥体都具有内切球。好,接下来带公式就行了,其中这个微锥呢,就是这个锥体的体积,三分之一的底面积成高,那 s 锥呢,就是这个锥体的表面积, 里面呢,你看是一个圆,那侧面呢?是一个扇形,把它加在一起就行了。接下来带入公式,你看耳内是不是有了,那接下来呢?不管是去求这个球的体积,还是求这个球的表面积,你直接带公式嘛,你看,我们只需要做这一道题, 体内切球的问题就通通结束了,只要你不算错,就一定没有任何的问题结束了。
2.0万高考数学高分思想陈晓 05:06查看AI文稿AI文稿
05:06查看AI文稿AI文稿我们来看四棱锥的内切球半径的通用解法,等你学会了之后,别说四棱锥,五棱锥、六棱锥,任意的棱锥都可以求助他的内切球的解法,一法解决所有问题。我们看 说四龙锥底面 abcd 是正方形,边长为 a 哦, aaaa, 然后呢, pb 等于根三 a, 这个是有点奇怪,谁会与有根三 a 有关呢?正方形的边长这个 a, 那么对角线是根二 a, 这是根三 a, 不知道怎么用。先往下看, 说 p d 等于 a, p d 等于 a, p a 等于 p c 等于根二 a。 我们发现了哦, p a, p c 与 a c 是相等的,原来这个三角形是等边三角形呀,不知道怎么用。继续往下读说 p d 是四棱锥的高哦, p d 与这个地面 a、 b、 c、 d 垂直的。我们又知道 a, b, c、 d 是正方形呀,那这样一来的话,你有没有发现了,这就是个强角问题吗? a、 d 垂直于对面, c、 d 垂直于左边平面, p d 垂直于底面,不知道怎么用。咱继续往下读,在四棱锥里放入一个丘 球,球的最大半径,我们想想一下,在这里面放入一个球不能跑出来哟,那要想让球最大,那不就是这个球和这个四棱锥刚刚相对,是相切,那这就变成了球四棱锥的内切丘半径。我们先把那些球的球心 大致的舍一下,因为相切问题呀,这个球画不出来。我们想象一下,这个球肯定与各个面都刚刚好挨住,这有一个唯一的缺点,那跟 立切的定义可知,这个小半径一定与各个面是垂直的。我们来看看这个正,这个四棱锥有多少个平面呢?正四棱锥有四棱锥, 四个侧面,一个底面,一共五个面。那这样的小半径一共有五个,我画不出来,我就不画了,我只画了两个做代表。你一定要明白,他是有五个小半径,那怎样求着小半径的大小呢? 这没有办法呀,因为他和别的线段直接联系,不容易找,也许有的好找,但是有的面呀,太不好找了。所以有一个通用解法,你听说过吗?那就是等提及发。 因为这小半径与各个面都是垂直的,那么我们只需要以一千元粗心 s 为顶 点和各个面为底边,构造一个一个的小棱锥,就把大四棱锥切成了五个。一定要注意啊,是五个小小棱锥,那他们的总体积是一定的。于是我们就得到这么一个数量关系,好意思先表达一次, 先把意思写出来,嗯,半径最大就是相切,相切的时候与各个面都有唯一的公共点。所以说这个小半径与各个面是垂直的,可以看作各个面上的高。那各个面为底边,他为高的小棱锥,正好把这个大四棱锥 分成了五个小棱锥,他们组成了大小棱锥,那么他们的体积就是相等的。下面的问题就是一个一个表示体积 啦,我们来看一看,一个一个表示大的。 a、 b、 c、 d 是正方形。已经知道了冷场是边长是 a。 这个题记好求,再来看看 p a、 b 这个三角形的面积好不好,求求 p a、 b。 先看形状,其实我们很容易可以证明 p a、 b 是直角三角形,但是这个题啊,移植线段太多了,我们懒得正,那就用线段吧。 p a 题目中交代过,等于跟二 ab 等于 a, pb 等于跟三 a, 你想一想,他们仨是不是关系很奇怪呀? a 跟了 a 跟三 a, 让你想到了什么?对勾果定理,那同理, pbc 是不是也是这个样子呀?你们的数字太奇怪了,连证明都不用正。其实我们当然可以证明,比起垂直于平面, pdc 比起垂直于 pc, 但是呢,不用正,直接可以得到了。好,各个侧面的面积也迎刃而解, 这样一来的话,各个小体积都可以表达出来了,然后两边三分之一越去,两边的 a 平方也越去,就可以得到这么一个小关系。所以说呀,求的半径就可以得到。 所以呢,这就是所求求的最大半径,你看明白了吗?扑通的棱锥,三棱锥也好,四棱锥也好,五棱锥也好,六棱锥也好,他的内切球的半径通通用的是等体计法,等体计法的本质是每一个小半径与各个面,各个面是垂直的, 所以他能分成几个小棱锥,就看他有多少个面,不要重复,不要一漏,熟的时候一定要一面一个面一个面的与球形连接。 为了让大家看得清楚,图形上呀,我没有连接那么多,所以呢,大家看图的时候要联想一下。好,请听下一题目。
 08:56查看AI文稿AI文稿
08:56查看AI文稿AI文稿各位同学大家好,那么咱们今天呢主要一起来学习一个新的知识点,就是关于人追的一个内接球的球半径,怎么去求解呢?其中有个公式就是 人均的一个内切球的球半径,按呢会等于这个人均的三倍的体积,然后再除以呢这个人均的表面积啊,这公司怎么推导过来的呢?我们可以一起来举个例子啊, 我们先来画一个 正,我们先来画个正方体啊, 嗯,这是一个正方体,我们现在呢一起来 标记一个那个的三人锥,比如这是 p, 这是 a, 这是 b, 这是 c, 好,我们可以把它的姓连接起来。 我们现在如果想求这个三人锥 p, a、 b、 c 的一个它的一个内切球的球半截,可以怎么去求解呢?我们可以把内切这个内切球的球尖给它标记标记出来,看到 o 点, 其实咱们说可以去连接 a o, 连接 c o 啊,以及去连接 d o, 所以我们这种情况下,当然我们还在可以再连接一下这个 p o 啊,那么这样的话,我们是不是就可以把什么把这个三人锥 p、 a、 b、 c 分割成了三个呢?而四个人锥对不对?所以因此如果我们想去求这个三人锥 p, a、 b、 c 的体积的话,他其实是不是等于三个小三人锥的体积之和,所以他就不可以等于三分之一的 s, p, a, b, c 乘上那些球的半径二,然后呢加上呢二分之一的 s, p、 b, c, 然后再乘二,然后加上呢三分之一的 s, p、 a、 c 乘上的半径二,然后呢再加上 s、 a、 b、 c 乘上的半径二,谁能把它合在一起的话,它是不是就可以等于三分之一的表面积? 因为就是或者你我们可以写一下三分之一的二,对,然后呢再把呢这四个 表面积加起来总往看着 s, 所以因此的话,我们现在想求这个外切内切球的半径二的话,是不是就可以等于三倍的体积除以 s 呀?好,这个公式的由来就是这么来的哈。 啊,所以呢,同学们一定要记得对于人均的内切球球半径的话,就会等于嘛这个人均的三倍的体积,除以什么啊?除以表面积啊, 我们可以一起来看一下这道题啊,那么这道题呢,它是说有一个正式人追啊, 咱们可以先画出一个 正式连接的一个图啊, 啊,这是一个正式连接啊, o, a, o, a, b, c, d, 嗯,这是 o 点,然后这是 a 啊, b, c, d, 我们现在呢要求什么呢?要求这个 它的一个 o, a, b, c, d 的内切球的表面积,所以根据我们刚讲的公式的话,它的 它的一个半径二的话,就会等于三倍的体积除以 s, 所以对我们而言的话,我们想求它那那些球的表面积的话,我们就得把它的一个半径求解出来, 我们先录下来看一下,就是我们怎么能把它的一个半径,就是我们讲的求出来的话,我们就需要把它的体积,体积我们知道肯定可以求出来,因为他的体积告诉我们是等于十二,所以怎么样去求他四个,呃,应该是五个面的密集之和, 因为我们说所谓的正式等级是什么?是呢,他的侧面都是呢,全等的等腰三角形,里面是正方形,而且他顶点呢,会投影到什么 a c 跟什么对角线, a c 跟 b d 的终点上面嘛?啊,这是它同一个点嘛?比如这个点同一个点,我们看是 o 撇吧。啊,那因此的话,我们把这样的几个题称作正式门锥, 所以我们是不是可以把什么呢?把 o o k 给它连起来啊? 我们现在目的呢,就是要去求他侧面的嘛,表面积啊,我们可以先求其中一个三角形的秘籍,那另外另外三个三角形的秘籍都一样的啊,所以我们看一下怎么去求 其中一个侧面的表,呃,表面积呢?好,我们来看一下,比如说我们就以求这个三角形 o b c 三角形啊, o b c 的一个表,呃,它的一个面积吧。啊,我们先如果想求它面积的话,我们得把它的底知道,因为底连告诉我们是边长 o b 杠二三嘛,对不对啊?都是 o b 杠二三啊。 然后的话,因为我们知道它告诉我们整个的一个体积为十二,人均的体积是等于三分之一的,什么 底面积乘以高等于十二,所以因此的话底面积乘以 h 会等于三十六,所以我们可以算出高 h 是不是可以等于三十六除以它的底面积, 因为它引杠底面分成 l b 杠三,它的平方的话就是就十二嘛,所以因此是不是三十六 给它除以十二是等于三,所以我们就可以知道 o o p 就是就是 h 是不是等于三啊?我们这时候可以呢去取呢 b c 的终点, 比如我们以它为地点吧,我们是不是可以去连接 o d, 然后再去连接呢? o d, 那么这样是不是可以构成一个直角这样形对不对啊?所以呢,我们可以知道 o、 o 撇是等于三,什么时候可以去求出 o 撇 d 呢? 好,因为我们知道他是一个底面,是一个正方形,所以我们可以知道这个角呢是四十五度,那这个角呢?也是四十五度,所以我们是不是可以知道 此时的话 b、 d 的话就会等于 o 撇 d 嘛?所以因此我们可以知道 o 撇 d 那个应该是等于什么呢?等于根号三 啊,因为我们说底面 b、 c 是等于呃被根号三,那 b、 d 就是等于它的一半等于根号三啊,所以我们是不是可以求得? 嗯,可以求得这个 o、 d 的话,是不是就可以等于根号下三的平方加上呢?根号三的平方,也就可以等于呢?根号十二,也就是二倍根号 三。好,所以我们可以知道它的一个侧面的三角形的高为二倍高三,所以如果我们想求这个三角形 o、 b、 c 的面积的话,就可以等于二分之一的什么 b、 c, 也就是二倍根号三,然后再乘高也是二倍根号三,所以它的的值的话就可以等于多少呢?我们可以把二跟二约掉,那根号三乘高三等于三,那是不是等于六? 嗯,水因石的话,整个的四个侧面的呃面积的话,是不是就等于四乘六?我们来再加上什么呢?再加上整个的底面 a、 b、 c 的面积是不是等于十二?对,所以加起来是不是也等于三乘六啊?水因 的话,我们是不是可以求得这个内切球的半径 r 的话就可以等于多少呢?我们可以写在这里啊, r 是可以等于三倍的体积 除以总共的表面积,所以呢,是不是三乘十二,然后再除以三十六等于一,所以这样我们就可以求那些球的半径二等于一,因此的话,它的整体的一个 球的表面积是等于四派嘛?二的平方也就等于四派嘛,所以教你答案就是四派,同学你学会了吗?
168乐学高数
猜你喜欢
- 1122潇洒的数学




