三角形的内切圆怎么画乐乐课堂
粉丝41.4万获赞227.6万
相关视频
 01:18
01:18 00:50
00:50 03:53
03:53 02:49
02:49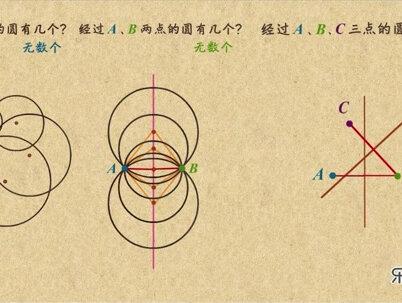 02:25查看AI文稿AI文稿
02:25查看AI文稿AI文稿这有个点,那经过 a 点的源有几个呢?这个源经过点 a, 这个源也经过,这些源都经过,看来经过一个点的源有无数个。 那经过两个点的呢?这个圆经过点 a 和点 b, 这个圆也经过,这些圆都经过,看来经过两个点的圆也有无数个, 但发现没,这些圆心都在一条直线上。我们知道,点 a 和点 b 到这些圆心的距离都是相等的,所以这些圆心都在线段 ab 的垂直平分线上。 那经过三个点的呢?根据刚才的分析,我们知道,经过这两个点的圆的圆心一定在这条线段的垂直平分线上,而经过这两个点的圆的圆心也一定在这条线段的垂直平分线上。也就是说,经过这三个点的圆的圆, 圆心既要在这条线段的垂直平分线上,又要在这条线段的垂直平分线上,那只能是他俩的焦点了。所以你以这个焦点为圆心,以这个点到这三个点的距离为半径,就可以画唯一的一个圆。 看来三点能唯一确定一个圆。其实这个圆也可以叫做三角形的外接圆,因为如果你把刚才这三个点顺次相连,就恰好能构成一个三角形,于是这个三角形外接圆的圆心也叫做这个三角形的外心。 不难看出,三角形的外心到三角形的三个顶点的距离都相同,到这两个点的距离相同,就是在这条边的中垂线上。到这两个点的距离相同,就是在这条边的中垂线上,而到这两个点的距离相同,就是在这条边的中垂线上。所以外心其实就是三角形三边中垂线的焦点, 刚才的撒点不在一条直线上,所以恰好能确定一个圆。但如果他们在一条直线上呢? 同样经过这两个点的圆的圆心一定在这条线段的垂直平分线上,而经过这两个点的圆的圆心,也一定在这条线段的垂直平分线上。但这两条线平行,没法相交,所以经过同一条直线上的三个点是不能做圆的。 好了,到了总结时间,不在同一条直线上的三个点能画出一个三角形,且能唯一确定一个圆, 这个圆就叫这个三角形的外接圆,它的圆心就是三角形的外心,这个外心其实也就是三角形三边中垂线的焦点。怎么样,明白了吗?如果明白,就快快刷题试试吧!
3242乐乐课堂天天练-初中数学 46:36
46:36
猜你喜欢
- 1066小玉老师
最新视频
- 36.9万圆梦数学 邪帝












