如何画角平分线
角平分线定理也是评论几何终结三角形的一个小技巧。上两期我们讲了三角形中线模型的两个结论,接下来我们谈一谈角平分线模型。首先要提的就是角平分线定理。角平分线定理的内容很简单, 我们先画一个三角形,如果一定是角一的角平分线,那么就有如下等式成立。同样吧,如果我们得知了这个等式成立, 也可以推倒厨卫迪士脚平分线。这个地理是如何证明的呢?那就听我娓娓道来吧。我们首先提炼出已经知道的条件一定是三角形的角平分线,那么就可以知道角一和角二是相等的,同时角三和角四手互鼓角。对于三角形, 必定我们可以利用正弦定理转化成这样的等式。对于三角形 adc, 我们同样可以通过正弦定理推的一个等式,结合已经体现出的题目条件,可以推导出较一的正弦值等于叫二的正弦值, 角三的正弦指也等于角四的正弦指。带路上数两个等式上面化解一下,我们就可以得到最终的角拼分析定理了。今天你有没有听懂吗?关注我,给你带来更多有用的知识!
粉丝127.0万获赞1102.8万
相关视频
 00:38查看AI文稿AI文稿
00:38查看AI文稿AI文稿cad 如何画角平文件?方法一,输入构造线的快捷键 xl 空格,选择二等分,输入字母 b 空格指定角的顶点,捕捉端点指定角的起点,点击直线上的端点,再指定角的另外一个端点 空格确认,这样角平分线就画出来了。方法二,输入 cl 空格,选择第一条边,选择第二条边,这样也能画出角平分线。这种方法画出的角平分线,我们改变直线的一个角度,角平分线也会随着变化。
374CAD宝哥课堂 01:50查看AI文稿AI文稿
01:50查看AI文稿AI文稿好,同学们,我们这节课来讲解一下如何利用此规做一个角的角平分线。好,我们看这里已经有画出来一个角 a, 我们利用圆规和尺子来做出角 a 的角平分线。首先我们打将圆规打开,将一个角的顶点放在 a 点这里,然后打开任意长度的半径,从这里画一条弧线下来, 得到两个焦点,这两个焦点我们待会再命名给他,这个是角低点,这里是角低点。然后的话,我们从低点这里将一个圆规的顶点放在这里,弧度保持不变,再在这里画一条弧度,也就是 圆规,他这个半径不要变动。然后同样道理到逼着点再画一条弧线,这两条弧线就会得到一个焦点,这个焦点我们命名为西点。 好,我们连接 ac, 就是这个角 a 的角平分线,我们连一下。 好,我们看一下我们这个 ac, 这个点 c 点角这条直线 ac 就是角 a 的角平分线。 那为什么 ac 可评分这个角类呢?我们下节课讲解一下他的数学逻辑, 他的原理是什么?我们通过什么样知识去证明一下 ac 就可以平分这个角 a。
3133邱老师讲志愿 07:41查看AI文稿AI文稿
07:41查看AI文稿AI文稿同学们好,欢迎来到大众数学,那么今天呢,我们来学习角平分的线来做图, 那么有了前等三角形的知识,那么我们呢,不仅可以把角平分的线做出来,而且呢我们还可以解释角平分线呢做图原理。好,那么在平面上呢,我们有这样一个角,是吧? 好,那么现在呢,我们要做这个脚的脚平线,我们知道要做一条线,那么我们至少需要两个点,是吧?好,那么这里呢, 因为他是角平分线,所以呢,他一定过错 o 点,所以呢,现在呢,我们有了一个点,那意思呢,我们还需要在里面再找一个点,然后呢把他们连起来啊, 那怎么样才能够找到另外那个点呢?啊?我们可以先用一个草图啊,我们先 这样看一下啊,比如呢,这个脚,我们知道两个三角形全等的话,那么他们的对应脚 是相等的,是吧?那你看啊,我可不可以让这两条线段,比如说 a 字 b, 可不可以去这两条线段相等呢?这是可以的,是吧?啊,我们用圆规呢啊,我们 这样画一条浮下来呢,好,我们就得到了这两条线段相等啊,好,那么然后呢,我们再来里面找一个点,那么这一个点呢,他到 a 点的距离和到 b 点的距离呢?是一样的。好,比如说啊,我们你看 好到 a 点的距离是这么长,然后我让他到 b 点的距离呢,也是这么长。好,那这样呢, 好,我们就找到这个点了,是吧?好,然后呢我们把它连起来,好,那连起来,好,我们就说这一条就是这个角的角度线,那为什么是呢?因为刚才我们讲了, 这一条跟这一条怎么样啊?也是相等的,这一条跟这一条呢,是相等的,然而他们两个还有一条什么拱共边,所以呢,这个三角形跟这个三角形怎么样?全等是吧?好,那既然全等了,非因脚相等, 所以呢,这个脚跟,这个脚呢就相等了。好,那么理由在这里,现在呢,我们就把它做出来了啊,那么方法我们已经有了,首先我们 o 这个点呢,为圆心啊,随便取一个长度为半径是吧?好,然后呢,我们这样做,你看现在是不是有两个焦点了啊?比如呢,我们用 o a, 这是 ob, 我们知道 oa 跟 ob 肯定是相等的,是吧?他都是这么圆的半径。好,那接下来呢,我们用以啊织一个 a 点为圆心呢,我们再画一条红。 好,当然这个距离呢,我们稍微把它啊弄长一点,那到底多长呢?至少是 ab 距离的 一半,比他还一半要大一点啊,比 ab 得一半要大一点。为什么是这样呢?因为这样呢,我们才能保证他有个焦点啊,你看,就刚才我们以这个距离就可以了, 那么这样呢,就有了一个焦点啊,如果我们把它 弄得太小呢啊,这个距离太短呢啊,他就不想教了,是吧?啊?不想教了,那不行,我们稍微把他弄大一点啊,只要比 ab 的一半大就可以了,他就有教练了啊,好,那么现在呢, 另外这个点我们把它打爆。好,接下来我们就把它连起来,是吧?那接下来呢,我们就把这个点 欧典曼连起来, 那么这一条线啊,我们把它称为啊 m 吧。好,那么 om 这一条线呢,就是这个角 aob 的平衡线啊, om 是角 aob 的, 品尝一下。 好,为什么是贫困县啊?刚才我们解释过了啊,我们可以利用钱等三角形把它证明 出来,是吧?啊,你看我们只要把什么这两个点点起来, 好,注意啊, om 指的是这条射线啊,那么这个点呢,我们也把它命名的角度试一点。好,你看, 我们把他的条件写出来啊,这个上面写,我们知道字一边跟字一边相等,是吧?啊,也就是 o a 等于 o b, 然后呢?自营边呢?跟自营边也是相等的啊,也就是 a c 等于 b c, 好,然后呢? o c 是公共边啊, 巩固别人啊, oc 等于 oc, 巩固别人也要写,是吧?好,那么说明这两个三角形啊,三角形 o, a, c, 我这个三角形什么呢? o, b, c 这两个三角形的三条边对应相等, 那既然这两个三角形呢,三条边对应的吗?所以这两个三角形怎么样啊?全的。好,我们的判断方法是颠颠颠。 好,那么既然这两个三角形前等,所以呢,我们就得到什么对应角枪的啊,比如是角一,角二,那所以呢,角一等于九二。好,那么这样呢,我们就可以把这个 角平分线做出来,是吧,那么这就是角平分线的做法以及他的原理。好,那么这节课呢,我们就到这里,再见。
40大众数学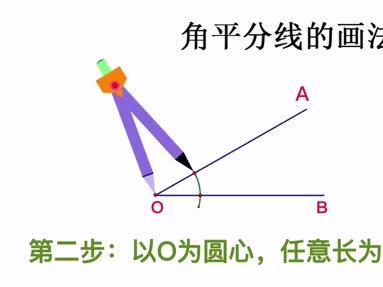 00:53查看AI文稿AI文稿
00:53查看AI文稿AI文稿第一步,画一个角。 第二步,以欧圆形任意长为半径画弧。 第三步,分别以 c 和 d 为圆,心大于 c, d 的一半为半净化壶。 第四步,连接 op。
124樊fan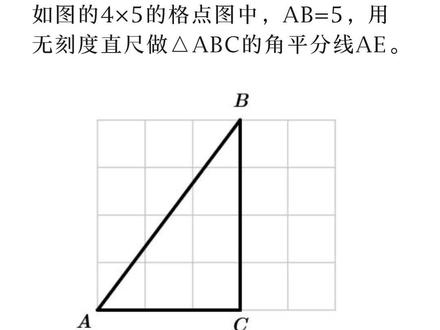 02:30查看AI文稿AI文稿
02:30查看AI文稿AI文稿在如图的四乘以五的隔点图中, ab 等于五,用无刻度的直尺做三角形 abc 的角平分线 ae。 我们在课本上学过用圆规来做一个角的平分线的方法,而在隔点图中,圆规跟两脚气都是不能使用的。那怎么做角平分线呢? 一种思路是把角的问题转化为边的问题。我们知道等幺三角形有三线合一的性质,如果点 a 是等幺三角形 a、 b、 c 的顶点,要做角 a 的平分线,我们只需要取底边 b、 c 上的终点 m 连接 a, m 就是角 a 的平分线。 于是画角平分线的问题变成了画终点的问题了。本题中按照这个思路,做角 a 的平分线之前,先够等腰,让角 a 的两 条边 a、 b、 a、 c 相等。题目已知 a、 b 等于五,而 a、 c 等于三,因此延长 a、 c 到地点,使 a、 d 等于 a、 b 等于五,那么角 a 变成了等幺三角形 a、 b、 d 的顶角。接下来我们的任务是找到底边 b、 d 的终点 m。 这里我们先介绍一下在格点图中画线段终点的方法。第一种情况,终点刚好落在某个格点上,这种最简单,什么也不用做,眼睛看准就行了。 第二种情况,终点并没有在隔点上,却在某条隔点线上,这种情况下无需划辅助线标出线断跟隔点线的焦点就是终点。当然,还有第三种情况, 终点可能在某个格子的中心。这种情况下,我们画出 ab 所在长方形的另一条对角线 cd, 那么 ab 与 cd 的焦点就是终点 m。 好了,我们现在要找到 bd 的终点 m 不难,用眼睛看出 m 点刚好落在一个格点上, 我们连接 e、 a、 m, 由于 a b 等于 a d, 所以 a m 平分了角 b a d 也就评分了角 b a c 取 a m 跟 b c 的交点 e, 则 a e 就是三角形 a、 b、 c 的角平分线。 最后我们总结一下,在隔点图中,若要坐脚平分线,请记住一句话,坐脚平分线,先坐等腰。
207春雨知行 00:45查看AI文稿AI文稿
00:45查看AI文稿AI文稿假如 cad 画角平分线有段位,你是什么段位呢?青铜,输入圆的快捷键。 c 空格,指定角点为圆心,画一个辅助圆,输入 tr 空格,两次修点多余的圆弧,输入直线。 l 空格,指定角点为起点,圆弧的终点为端点, 画一个辅助直线,这个直线呢,就是角平分线。黄金,输入 xl 空格, 输入 b 空格,指定角的顶点,指定角的起点,指定角的端点,这个构造线呢,就是角平分线。王者输入 c l 空格,选择第一条直线,选择第二条直线,这样角平分线就画出来了,你学会了吗?
962CAD教学_宝哥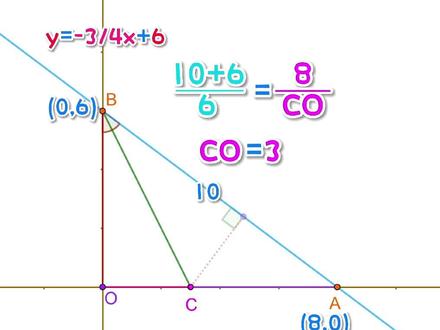 00:52查看AI文稿AI文稿
00:52查看AI文稿AI文稿平面直角坐标系内角平分线,如何计算?直线 y 等于负四分之三, x 加六与 x 轴和 y 轴分别交于 a、 b 两点角 a、 b、 o 的平分线交 x 轴与点 c, 求点 c 的坐标, 根据解析式求出 ab 两点的坐标以及 ab 的长度。根据角平分线定理, ab 比 bo 等于 ac, 比 co, 两边同时加一并通分 ac 加 co 又等于 ao, 即可求出 co 等于三。 即使 bo 与坐标轴不平行,依然可通过勾股定理求出 bo 的长度。同样的方法求出 oc 的长度,再根据点 o 的坐标即可求出点 c 的坐标。
1092智小优 00:42查看AI文稿AI文稿
00:42查看AI文稿AI文稿角平分线怎么做?以顶点为圆心,任意长度为半径画圆弧,交角两边两点以大于两点间距离一半的长度为半径,分别以两点为圆心画圆弧,使两段的圆弧交于一点, 连接该点与顶点,就是该角的角平分线。那为什么这样做就是角平分线呢? 因为这两段是同一个半径,这两段也是同一个半径,所以这两个三角形是边边边情况下的全等三角形,所以对应角相等,所以他是角平分线。
2064张解数学 07:34查看AI文稿AI文稿
07:34查看AI文稿AI文稿今天我们讲解如何在圆中画一个角的角平分线,那么首先这个角相对来说会有一定的特殊性,他其中一个边是直径,另外一个边是一条弦, 那么此时如第一个图三点 a、 b、 c 均在格点上, bc 是一条直径,那么如何来画这样角 abc 的角平分线, 也就是说我们需要在 a、 c 弧上找一点 p 连接 b p, 使得 b p 是角, a、 b、 c 的角平行线,那么 根据这句话,我们得到的这个 p 在弧 a、 c 上,那么根据我们所学的圆里边的知识,有一个等弧对等角, 等弧对等角,因此这个点辟应该是 a c 弧的终点, 这个 a 是一个格点, c 也是个格点,但是它这个弧我们想找它的终点去, 不能直接通过这个格点上面直接看出来,因此我们需要另用到另外一个知识,吹荆定理。 圆当中垂径定理是怎么定义呢?过圆心的 直径,如果垂直弦平分弦、平分弦所对的弧,那么这时候刚好符合我们想要的这个弧 ac 的平分弦 平分的这个终点,因此我们需要去找的就是 ac 这个弧的终点,那么我们需要先连接 ac, 我们先找 ac 这个弦的终点,那么由于 a 和 c 都是格点,很容易在这我们看出来 它与隔线交的这个点,如果说是点 d, 那么它就是这个 弦的中点,那么这时候我们如想找这个 垂直这个弦的什么呀直径,因此我们还要找圆心,那么此时我们发现这个圆比较特殊,我们现在已经过了三个, 三个格点,所以说我们想去找圆心还是比较好找的。由于 b、 c 已经是直径了,那我们发现这两个点 相连也是直径。因此如果说这俩是 e、 f, 那么它和 b、 c 相交于点, o 既是直径,既是圆心,那么此时圆心和地相连并 延长,那么交 a、 c 互引点 p, 此时我们连接 b、 p, 即为我们相求的角 a、 b、 c 的角平分线。 这个是咱们讲的第一种方法,这个比较特殊,你会发现 a 和 c 都是格点,所以我们找它的弦的终点比较好找。那么你看第二幅图, a、 b 仍然是直径,那么此时这个 b、 c 在这时候它不是一条线, c 在这个半圆的外围,那么因此即使我们现在知道了 b、 c 与 圆焦的这个点,那么这个点也不是一个特殊点。所以我们如果 连接 a、 d 的情况下,你会发现这个 a、 d 呢?我们没办法去找 a、 d 的终点,所以因此我们就不能用刚刚的那个方法去找弦的终点。 那么这个里面比较好判断的是,由于 a、 b 是直径,所以也比较好判断的是这个点是一个圆形。 我们知道圆心 o 之后呢,在这里我们连接 o、 d, 那你会发现这个 o、 b 是等于 o、 d 的,原来这也就是这个角是等于这个角的 角 obd 等于角 odb。 那么此时在这个图里边,我们就想找的还是谁呀? ad 互的重点。 那么此时如果我们做过点 o 做 b、 c 的平行线,这个 b、 c 呢?它比较好判断,它是横二纵五,横二纵五,因此我们 过 o 去做 b、 c 的平行线,那么应该我们找横二纵五,那横二同样这纵五一二三四五,也就这个格点的终点,因此 我们只需要连接它的一个矩形对角线,如果说这是 e、 f, 那么他与格点交一点格线,交一点 g, 那么此时我们连接 og, 那你会发现此时的 og 他就会平行 bc, 那平行 bc 之后,此时你会发现这个角和他是一个内错角, 也就角 g、 o、 d 和 o、 d, b 是一个内错角,它两个相等, 他们两个相等。那么由于根据圆当中咱们有一个支点叫铜弧,所对的圆心角是圆珠角的二倍, 因此我们发现角 a、 o、 d 应该是角 a、 b、 d 的二倍。那么现在我们又找到了 g o, d 是等于角 a、 b、 d 的, 所以我们就找到了此时的 og 就是角 aod 的角平分线,它是角平分线,因此我们也就发现了这个 og, 它与弧 ad 的交点 p 正式弧 a、 d 的中点,因此我们再连接 b p, 所 b p 就是我们要找的角 a、 b、 d 的角平分线。
42杨老师
猜你喜欢
最新视频
- 3851铭品数学









