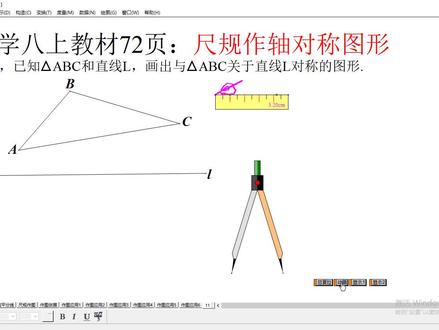
数学初二年级上册72页的图案怎么剪

新阳老师带你一条视频，详细解读八上全等三角形五大辅助线思路。 全等三角形是初二上学期当中一个最难的章节，也是我们初中几何的一个正式开端，更是初中数学两级分化的一个开始。 很多同学对于全等三角形来说，他不会去做辅助线，不会去构造全等三角形，那今天轩老师教大家全等辅助线的五大绝杀思路，我们来看哪五个思路？第一个思路就是利用公边去构造全等三角形。第二个，我们可以通过倍长线段，也就是倍长中线或者类中线去构造全等三角形。 第三个，通过截长补短的方法构造全等三角形。那第四个方法遇到我们的角平分线加上垂线 垂直的条件，这个时候我们可以通过什么延长去构造对称型全能？那第四个，如果出现了角平分线，并且角平分线上的一个点 做了另一边的垂线，那这个时候我们可以做另一边的垂线去构造对称型全能。那具体是怎么去应用的呢？我们通过几个题来给大家具体展示一下。 那首先第一个我们利用公共边去构造全等三角形，那这道题目当中出现了什么？出现了 a、 b 等于 a， c， b， d 等于 c、 d， 所以 这时候我们来标注一下， a、 b、 a、 c 是 相等的，然后 b、 d 和 c、 d 是 相等，所以这个时候你会发现，我只要再创造出一个公共边，也就是我只要连接上 a、 d 之后就会出现什么？就会出现两个三角形当中三组 边对应的边完全是相等的，那根据我们 s s s 我 们就可以得到这两个三角形是全等三角形，那两个三角形全等了之后，就可以得到角 b 是 等于角 c 的 了，对吧？那角 b 等于角 c 了， 那并且告诉你了角 a 等于多少，角 d 等于多少，所以这个时候通过四边形内角和直接就可以求出角 b 的 度数。完事了啊，这是第一个，我们如何去利用公边构造全等三角形？ 那第二个类型，倍长中线构造全能，也就是我们刚刚说的叫倍长线段去构造全能三角形。那这种类型题的一个明显性的标志就是在题目当中出现了与中点相关的线段，那比如说这道题目， 这道题目它说已知 c、 d 等于 ab， 然后告诉我们 b， a、 d 等于 b、 d， a 这俩角是相等的。好了，关键性的条件叫做 a、 e 是 三角形 abd 的 中线， 所以出现了中线啊，与中点相关性的线段，这个时候我们就可以通过去倍长中线或者类中线构造全等三角形。 那这道题我们如何去构造辅助线呢？那因为 a、 e 是 a、 b、 d 的 中线，所以 a、 e 是 一条中线，那这个时候我们可以什么延长？ a、 e 叫做加倍延长，它我们叫做倍长中线嘛，所以什么叫倍长中线？就是加倍延长，那所以这个时候 a、 e 和 e、 f 它俩变成相等的。好，我再连接上 f、 d 之后，这个时候你就会发现这两个三角形就是全等三角形，对吧？然后我们再根据题目当中的已知条件，可以推出来这两个大的三角形也是全等三角形，那进而就可以完成这道 题目的一个证明，所以这是这类辅助线的一个构造方法，我们叫做什么？倍长中线或者倍长类中线？如果题目当中出现与中线与中点 相关的线段，你就可以考虑可以把它加倍延长，然后构造出全等三角形，进而完成题目的求结。好，我们再来看一下第三类， 那第三类叫做截长补短法，去构造全等三角形。那这类题目一个关键性的识别条件是什么呢？就是在题目当中出现了角平分线，并且出现了 线段和差关系的这样的一个关键性的条件，我们就可以考虑是不是可以利用截长补短的方法去构造全等三角形。 那这道题目我们怎么去截长补短？因为 b、 d 是 角平分线， c、 e 是 角平分线，对吧？所以这个时候我们可以去截取什么？在 b、 c 上截取一段线段 b f， 使 b e 和 b f 是 相等的，然后并且又有角平分线，所以马上可以证明出这两个三角形是全等三角形， 然后再根据它题目当中的已知条件，角 a 等于六十度，我们马上可以推出这个角和这个角啊，这两个角也是六十度， 然后这又是角平分线，这俩角又是相等的，所以马上又可以得到这两个三角形啊，这两个三角形是全等三角形，那进而完成我们最终这个结论的一个证明。好，这是截长补短的方法，构造全等三角形， 那关键性的信息是什么？叫做题目当中出现了角平分线，并且出现了线段和差的这种关系， 不论是这个和差的关系是让你求证的，还是题目当中已知性的条件？只要出现了这两个条件，你就可以考虑是否可以利用截长不短构造全等三角形，那这是我们第三个通过截长不短构造全等， 然后我们再来看第四个，第四个这种类型的题目是在题目当中出现了角平分线，并且有什么有角平分线的垂线的时候，那这个时候我们就可以去选择什么去延长这个垂线 c、 e。 好 了，延长垂线 c、 e 之后，那我们与边 b、 a 的 延长线相交于一点，这个时候你就会发现你构造出了一个对称性的全等， 那这个角是直角，对吧？然后这又是角平分线，所以这俩角是不是相等的？然后并且有个公共边 b、 e， 所以 整个两个大的三角形，那我写到这啊，那也就是我们的三角形 b、 e、 c 是 全等于我们三角形 b、 e、 f 的， 所以这俩三角形是全等的，这是我构造出来的对称性全等。然后再根据题目的条件，你还会发现你还可以证明哪两个三角形，证明这两个三角形 a、 c、 f 和三角形 b、 a、 d 也是全等三角形，这俩三角形也是全等的，那进而我们马上就可以证明出这两个线段之间的 倍数关系了。那这是我们通过什么遇到角平分线，并且对于角平分线什么上面它有一条垂直于它的线段，那我们就可以延长构造对称型全能，那一定要刮，一定要抓住我们题目当中的关键性的条件和信息。 好，我们再来看一下第五类，叫做垂法构造全等三角形，那这类题目有一个什么明显的特征呢？就是它在题目当中一定会给你关键性的条件叫做有角平分线， a、 c 是 我们 d、 a、 e 的 角平分线。 好了，然后这个时候还有什么关键性的条件？就是在角平分线上有一点它什么？它有到 角上的一边的这种垂线段，那这个时候我们就可以选择利用角平分线的性质去做出另一边的垂线，构造对称型全等，所以这时候我做出另一边的垂线， 那这个时候根据我们角平分线的性质，角平分线一点到角两边的距离是相等的，所以 c、 f 和 c、 e 就是 什么 就是相等的，并且还有什么公共的边 a、 c、 e， 然后这还有角，对吧？这俩角相等，然后这还有直角，所以你一定可以证明出这两个大的三角形就是全等 三角形，对吧？所以这是我们构造出来一个对称型的全等，然后进而再根据题目当中的条件去证明另外两个三角形全等，或者再证明其他的 三角形全等，我们就可以完成我们最终结论的一个证明。那这是我们根据什么根据做垂线的方法去构造全等三角形，那再来强调一遍它的关键性信息是什么叫做出现了角平分线，并且角平分线上一点有到另一边的这个 垂线啊？那这个时候怎么去做？我们做出角另一边的垂线，就可以构造出对称型全等，进而通过他相应的条件和结论，以及题目当中的另外的条件，我们可以去推出他相应的结论 啊，这叫我们利用做垂线的方法构造全等三角形，所以对于我们全等三角形而言的话，那掌握了我给你讲的这五类方法，很多题目都可以完成，求解。

在我胡叶本的第一页上，贴着这么一张简笔画。 我和他的故事大概要从初二那年说起。像是一次偶然的换座，我俩成了同桌。那时和他还不算熟络。 说实话，在那只青春懵懂的年纪，和女生同桌本就带着几分局促，何况他长得又那样好看。 起初我们没有多少交流，我的成绩还算不错，偶尔教教他几道稍显复杂的数学题。但同桌的日子久了，我们渐渐成了无话不谈的朋友。 自从和他坐在一起，我就这从前铿锵执手的纪律委员，竟成了上课跟他讲小话的坏学生。 有一次上课，连平时最疼我的物理老师都忍不了了，点了我们的名，让我俩一起站在教室门外，还笑着调侃了几句。 我的脸一瞬间红成了苹果。我知道，这份羞辱并不只是因为被老师批评的窘迫。 说实话，他的性子不算淘气，有些急躁，也不愿意轻易相信旁人，班里同学便给他起了虎妞的外号。这些我从他偶尔提及的儿时经历里也能听出几分。 父母早早离异，他跟着妈妈重组家庭，又遇上了不待见他们的哥哥。 我总说心疼他的过往，他却告诉我讨厌别人因他的家庭而同情他。那一刻，他在我心里竟显得格外挺拔。十几岁的年纪，这份不愿示弱的自立自强实在难得。 他待我却格外温柔，会认真听完我所有的碎碎念，也把我当成唯一能倾诉所有心事的知己。他总唤我真真，就多半源于我的外号老真吧。 那段与他的同桌的时光，一定是我人生里最鲜活也最快乐的岁月。 大概过了半年，老师便把我们调开了。后来因交流渐少，又添了些些琐碎的误会，我们渐渐疏远，最后竟彻底闹掰了。 但我们都清楚，彼此都会想着挽回这份来之不易的友情，可谁也没有先开口。 初中最后一天，老师让班干部上台给同学们发苹果送祝福，健忘的班主任竟忘了我也是班委，还是他在班里大声喊出了我的名字，老师才想起让我上台。 让我难以预料的是，这么多的班干部正好轮到我给他送祝福，但我却鬼使神差般的跳过了他。 他没有当场表露生气，只是后来听我的朋友说，他那天真的很伤心。 那句迟来的祝福，我最终写在了 qq 空间里，只是祝福的对象也没有表明，只是用问号草草代替。 我到底是什么时候开始喜欢上他的？说实话，我到现在也想不清楚。和他同桌时，我只当他是最好的红颜知己。 活到现在，我真心喜欢过的女生不过两位，他便是其中之一。我总觉得，真正的喜欢从不是被皮囊吸引， 而是看到了他灵魂里的模样，是他藏在急躁外折下的那份坚韧，是他不愿被同情的骄傲，也是他独独对我展露的温柔。 这些细碎又珍贵的特质，才是真正刻进我心底的东西。我想，也许是高考结束铃声响起的那一刻吧。自那以后，他永远成了回忆里的人， 我们再也没有见过面，可我总忍不住怀念和他同桌的那半年时光。 直到现在，我也难以释怀，那句迟到了的祝福成了我心底解不开的结。偶尔聚餐或谈心时提起他，我语气故作风轻云淡，讲述着关于他的一切。 我仍留着他，所有社交媒体的好友，却再也没有主动找过他，也不曾点开那个熟悉的头像去窥探他的生活。我太清楚放弃有多遗憾，但是有些温度本就应留在特定的季节。 时间终归是仁慈的，我的心也慢慢平静了下来。只是可惜，我们不该这样，却又只能这样。 也许某天想起他，我会笑着感谢那段相伴的时光，而被他改变的那部分的我，也永远留在了我的身边。