五年级上册数学67页图形的面积公式
这一单元我们学的是有关图形的知识点,那你在解决一道题的时候,你肯定第一点是根据题目当中的已知信息去把这个图画出来呀。你就在这坐着想想想你怎么想也想不明白, 所以第一步你要根据他的提示去画图。好,来,老师来画,看老师怎么画的哈。他说一个三角形,这个三角形有没有特殊的要求?等腰吗?等边吗?直角吗?有没有?没有说明就是一个一般三角形,那就随便画一个三角形,我画在这,他的底是六米 底,我以这一条边为底,对吧?啊,因为好画一些。来,接着来看,如果底边延长两米,面积就增加三平方米,他说什么我们画什么来, 先画底边延长两米,什么叫延长?你的指尺靠着他再多画出去两米,注意哈,你要看清楚,如果这是六的话,两米要短一点,是不是?来看老师怎么画啊?靠着我延长两米出去。 假如说这就是量你,你不需要去量,大概画一下。好,底边延长,其他的不动。他说面积增加,那面积的话要增加,说明他还是形成了一个三角形的,是不是?那这一点是没有动的哟,因此我要把这里延长起来, 这一步老师画的图的这一步能看懂吧?能,好,我把这个延长起来, 这个叫做底边延长两米,两米面积增加,请你告诉我增加的面积在哪? 缩出来的这一块面积是增加的几来三平方米。问,原来三角形的面积,那我们来看,原来三角形的面积在这,已知这个三角形面积是 a, 三角形的什么 底?那我们回忆一下,三角形的面积等于底和底,二底知底了,还差谁高?我把它的高做出来。高, 这条底对应的高。注意,你们在做高的时候要用三角尺去做哈。好,这是他的高。哎,这是我把的高,算出来那面积就知道了。那这个高是什么呀?同学们,看呢?看呢, 这个多出来的。呃,增加的面积是三平方米,这一段是底,二平二米。我发现原来的这个三角形的高,实际上也是增加的这个三角形的高, 能看出来不来,我看哈,原来这个三角形的高是没有问题的。那增加的这个三角形的高怎么画?如果以这一条为底的话,从对面这个点向他做垂直线段,因为这是一个蹲角三角形,因此我要把这个延长出去,延长到这, 然后从对面这个点向他做垂直线段。我发现做出来的高也是这一条,听明白了没有?好,那这条高怎么求呢?同学们, 这条格怎么求呢?来,我们先写一下公式哈, s 等于 a, h 除以二, 利用我们等式的性质,最后要得到 h 等于多少呀?是不是就像解方程一样,利用等式的性质,最终要把 h 留下来?现在我要把与 h 无关的先抵消掉。来,左两边先同时 乘二,左两边同时乘二的话,把这个除以二抵消掉了,左边变成了二 a 四,右边就是 a h。 老师减写哈,来,再来,我还是要剩下 h, 那 左两边再同时 除以 a 除以 a。 二 s 除以 a 不 就是剩下 h 了吗?因此,三角形的高怎么求? 面积乘二除以 a, 这是我们推算出来的高的高的这一个公式哟,再来一次,三角形的高怎么求? 面积乘二除以 a。 再来一次,三角形的高怎么求?面积乘二除以 a 相反,那我已知 s 等于 a 除以二,那我要求 a 等于多少呢? 能一下子看出来吗?二 s 除以 h。 反正要先把面积乘两倍,变成一个平行四边形,再除以对应的高和底。好,这一点搞清楚之后,我们就来求他的高 高怎么求?刚才说了,一二二乘三,一二等于三,哪位米?那这个高求出来就是三比零。现在简单了,原来三角形的面积说 六乘三除以二等于九平方米。来,我把小标题写一写,这个的小标题是高,这个小标题是来这个题,听懂的举手。 因此我们把这个公式请补充在书上啊。来, h 等于。先看老师写, 三角形的高等于说二 x 除以 a, 三角形的底等于二 x 除以 y。 把这两个公式再数上。
粉丝5.2万获赞16.0万
相关视频
 10:59查看AI文稿AI文稿
10:59查看AI文稿AI文稿刚才已经给它复制出了一个一模一样的梯形,那么你们想象一下这个梯形我怎么利用起来?转过来一下, 转过来,我们利用旋转的帮忙。好,是这样,是,然后我们给它挪过来的。拼接在一起。好,同学们,现在旋转拼接在一起之后,我们形成了本来是两个散的分散的梯形,对不对?现在拼在一起之后,它形成了一个平行平行四边形,形成了一个平行四边形。 好,老师在复制的时候呢,这老师复制的梯形它大小、形状是一样的,所以我们这里原来图形短的这条是上笔,那同样的,他复制出来旋转了一下之后,他变到哪里来了?上笔变到哪里来了?下笔这里是不是变的到?哎,他原来是上笔,他在这里他还是短的,所以还是上笔。对,他在这里还是上笔。 那同样的,这条长边是转到上面去,是,它是长的,我们都转到下底,所以它即使到上面去了,它也还是下底,还是下底好。所以通过拼接我们看出左边一号 梯形和右边二号梯形,它们两个的面积同样有,它是什么?左边梯形的面积是一号,右边梯形的面积是二号,颜色一样不一样。好, 左翻是我们发现一号图形和二号图形填满之后,刚好填满了我们的平行四边形,所以我们就可以得出平行四边形的面积,其实就是几个梯形,两个梯形,对,就是两个梯形的面积。好,我们来写 得出平行外面,外面是倒四边形,对,外面倒的平行四边形的面积,那它不是等于两个梯形的面积,是不是?是。好,我们一起平行四边形的面积等于什么?底的成高,它是等于底的高的。好, 那他现在一个平行四边形不是等于我们两个梯形的,两个梯形的面积。 好,那我们现在来进行细写,来看一下平行四边形的底在哪里? 平行四边的底在哪里?三三三,走吧。哎,太矮了。平行四边的底边是不是下面这条边?是,这条边是由一号图形的, 由一号图形的下底和二号图形的下底组成的,所以我们这里就可以写 平行四边形的底是由下,是由下底和上底组成的,但是呢,我们习惯性的把上底写在前面,那我们就说底,它是由上底加下底加下底。好,上底加下底, 它是上底跟下底加在一起,对不对?对,这个底应该是上底和下底的。哦,怎么记的?用括号做起来。好,继续。 然后成高呢?我们的高在哪里?高,是不是原来梯形的高?对,他们是等高的,因为上底下底是一条平行线,平行线之间他们的垂线线段距离最短,垂线线段就是这个梯形的高,同时他也是平行四边形的高,所以我就继续写成高。 好,这个上底加下底乘高是几个梯形的面积?等于两个梯形的面积。 那我们看哟,梯形的面积是要算面积的面积吗?不是,我们只需要求一个梯形的面积,所以这两个一模一样的。那我求一个的话,我还要怎么做?求你干嘛?求二,求二, 也就是说要把我们这个公式要给它进行平均分,把这个进行平均分,那就给他们直接把上顶加下顶的和再乘高拿来,我的第二,好, 也就看出来这就是几个梯形的面积。两,你可以说啊,是几个梯形的面积,一个对就可以得出就是一个梯形的面积,一个梯形的面积, 所以我们得出这个公式,梯形的面积等于什么?上底加下底,横叉带。好,我们再来看这一个, 同样呢,这个直角三角形也是一模一样的,形成了什么长方形?对,他拼接在起形成了一个长方形。行, 好,那么我们再来把它的名称往上调,原来的梯形短边是上底,现在我们算到下面,这里就是他原来的上底, 原来的下底会从左上面,对对对,就是他下下底,这是他的下底。好,我们来看第一个图形,好,我们左边我们给它叫为一号图形,一号梯形,好,右边给它叫做二号梯形, 我们紫色的这部分是我们紫色的这部分是我们白色的这一部分刚好。一号 面积和二号图形的面积填充满之后就是谁的面积。长方形的面积。对,也就可以得出一句话,在这里长方形的面积就是两个梯形的面积。对,好, 长,本来长方形外面是长方形,对不对?长方形的面积等于什么?长方形?长方形的面积等于长成宽。好,那 现在我们来测量长成宽究竟几个平行的面积,两个平行的面积,两个平行的面积,我们测量当然是只需要一个平行的面积,对不对?对,好的来转化, 对,转换长方形的长来,长方形的长在哪里?上,在下面这条,对,也可以是上面这条,下面这条他有第一个原来的梯形的下底和第二个图形的上底加在一起,是不是这个长的就换长了?对,就是说把长的换成了 上笔加下笔。好,我们加是我们的长是下笔跟上笔的和组合起来才是长。对,对,我们这里要用一个画表示的是上笔加下笔的和, 然后呢?他的宽的宽的宽怎么转换原来的宽?我们现在的宽是不是左边这条和右边这条是刚好,又是原来矩形的高?对,所以把长方形的宽转换成了高。 哎,这是几个面积的面积?两个面积的面积上我们只需要一个面积,等于两个面积的面积。 咦,好,我只用一个平行的面中,那变成什么样啊?除以二,那就变成预备停上底三下底的和,这怎么样?和,好,哎,这是两个平行的面,我要的是一个除以二,最后一个 这个三角形,这个梯形我们又如何来创造?如何来选择吧。好,进行分割三角形。哎,停停停,这个梯形被我给它。同样啊,分割分割成了几个图形?两个角形,两个图形都是三角形。好,左边 是一号,左边一号,右边二号,二号,换个颜色当然不一样。好,左边。我们来看,还是那句话, 把我们的梯形分割成两个三角形之后,我们来观察第一号图形的面积是不是紫色最快?是,二号图形是蓝色最快,紫色最快。 一号同学和二号同学填,给他填充之后刚好得到,我们刚好可以得到我们一个什么梯形面积。知道得到梯形面积。是,所以我们又可以得出一个结论,什么 梯形形的面,面形等于。哎,梯形面积等于什么?是等于两个三角形来相加,等于两个三角形,形 等于两个三角形的的面积。好,那么我们现在来进行转换, 第一个三角形它的面积是不是等于底乘高?是第一个三角形的面积等于底乘高。那怎么样 再除以二,再怎么样除以二。好,这是第一个小三角形,一号三角形。那二号三角形呢?二号三角形等于底,再加上二号三角形,底乘高也要除以二。好,朋友们,这里大家会区分一下,我们左边呢是 左边的这个是一号三角形,右边的这个是二号三角形。好,现在继续往下, 继续往下,现在来看我们谁和谁是共有的底?底和高,到底的底在哪里?一号三角形的底在哪里?上底是不是上底?对,记住一号的底就是上底成高,再除以二,加上。好, 二号的底在哪里?下底,三号的底在这,所以就是下底,这个底是下底, 也是要乘高再除以二。好,那我们现在可以得出,我们之前学过了,有乘,有他又有乘,其实就是什么乘法分配律。那把共同的因素给他提出来,谁是共同的? 高和除以二,高和除以二,共同的因素,我们就把它提出来,放到括号中,后面 写成勾除以二。二。好,那前面呢?还是谁前面是谁?上笔尖尖加谁下笔?第二个图形的下笔乘二,然后再乘勾除以二,出完了去 通过我们三个图形的转化,我们都可以得出同一个结论。什么结论? 梯形的面积等于上底加下底的合成,高半除以二,再看梯形的面积,哪边梯形的面积等于上底加下底的合成都不一样,再看这里是不是 梯形的面积,是两个三角形的面积,所以可以搞出来了,它就是一个梯形的面积,用字母表示,上底用 a, 下底用 a, b 高还是圆的那个用什么 a? 所以我们给它写出来就是 a 加 b 的 和乘再除以二。但是这里用不用写?不用这个,这个乘就像不用 就直接写成 a 型的面积,等于括号 a 加 b 的 和 s 除以二可以了,有问题吗?没有, 用字母表示为一个电瓶用 a 和 s。
55木易老师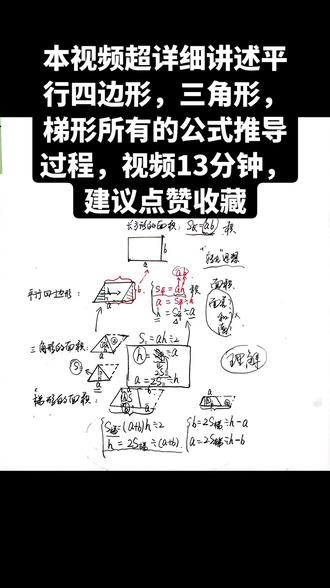 13:24查看AI文稿AI文稿
13:24查看AI文稿AI文稿本视频超详细讲述平行四边形、三角形、梯形所有的公式推导过程,视频十三分钟,建议点赞收藏!至此,我们这所有的公式一共十个,全部都搞定了,那哪十个呢?平行四边形三个,三角形三个,梯形一二三四四个,一共十个。 呃,今天我们来讲一下平行四边形、三角形、梯形的一个面积计算它的公式怎么去记忆啊?首先我们学数学啊,我们抛开死记硬背的这种模式啊,一切都在理解的过程中,那么今天我们会讲到一个方法,叫做转化思想, 什么叫转化思想?就是将我们复杂的东西变简单,将我们未知的东西转化成已知的东西啊,所以我们今天取的这三个图形的面积,我们从平行四边形开始,那么一切的源头都会从长方形转化而来啊。首先我们看平行四边形, 我们看到这里有个平行四边形,那么我们底用小 a 来表示,高用 h 来表示,那么长方形我们以前学过的,它的面积公式是 s 等于 ab, 对 不对? a 是 长, b 是 宽啊,所以这个是我们比较熟悉的,那么平行四边形的面积怎么计算呢?我们将平行四边形进行分割,把这一块往右边平移到这里, ok, 那 么这个图形就变成了什么图形,是不是长方形的样子呢?所以我们来比较一下,变成长方形的样子之后,那我们来看一下这条是不是长方形的长,这条是不是长方形的宽, 对不对?那么我们来看一下长方形的长和长方形的宽跟我们平行四边形有什么关系?长就是这条,这条同时也是 平行四边形的底,那么它的宽呢?就是平行四边形的高,对不对?所以我们这里算平行四边形的面积的时候,它就等于 a h, 其中 a 是 长方形的, 这个长 h 是 长方形的宽啊,是不是就对应成了?所以我们将平行四边形的面积转化为长方形来计算好, ok, 这就是将 未知东西换成已知东西啊,比较简单。那么这个是我们常规的一个面积计算公式,那么反过来,如果已知告诉你, 平行四边形的面积反过来求底,怎么求啊?那我们就用平行四边形的面积去除以高。那这里要强调一下,为什么我们在学新的一个东西的时候,有时候 一些新的名词解释的时候,这名词不是乱命名的,比如说我们在学这一单元叫做面积,那为什么他不叫面差呢?为什么不叫面和呢?为什么不叫面商呢?他偏叫面积呢?你会发现这个长方形,它的面积是不是 长乘宽?哎,长乘宽,它的结果是不是以 g 的 形式出现呢?然后这个平行四边形的面积是不是 a h 啊?底层高,对不对?是,也是以 g 的 形式出现的,所以才叫面积,不叫面和,面差、面商,对不对? ok 啊,那么既然是以 g 的 形式出现,那我们来看一下,如果说我要求一条底, 那么我是不是就是用面积去除一高?一个因素等于 g, 去除另一个因素,是不是很好记,对不对?那所以这里 h 就 等于平行四边形的面积去除以 d, ok, 那 平行四边形我们有三个公式,是不是相对来说比较好记一点。好,接下来我们来看三角形, 我们如图有一个三角形啊,要计算这个三角形的面积,我们将三角形的面积通过平行四边形的面积来推导啊,那么怎么得到三角形的面积计算公式呢?首先我们在实践过程中,我们会发现啊,任意一个三角形, 我只要画出它一模一样的三角形,并进行重新组合,就能形成一个平行四边形。那比如说这个三角形,我们将这个三角形啊,找到它一个双胞胎, 然后将它重新组合,它是不是就变成了一个啊?平行四边形对不对?那一号跟二号长得一模一样,我把二号脑袋倒过来放在这里,是不是就组合成一个新的图形? 那这个图形就是平行四边形,那我们来看一下三角形的底,我们用 a 来表示啊,三角形的高我们用 h 来表示,那么我们会发现这个三角形的底就是这个平行四边形底,这个三角形的高就是这个平行四边形的高,对不对?那么现在这个平行四边形的面积是多少?平行四边形的面积就是 h, 但是我们要求的是三角形的面积,怎么办?三角形面积是不是就是这个平行四边形的一半?所以我除以二。好,这就出来了第一个公式,三角形的面积等于底乘高除以二,那么这个相对来说比较简单。那往往有同学会问题出在哪里呢?就是这个 给你一个三角形,然后也告诉你他的面积,告诉你啊,告诉你一条底,现在呢,要求这条高是多少?那同学这个公式 就有点迷迷糊糊了, h 等于什么?其实很简单,我们还是将这个转化到平行四边形里面去求。我们刚刚求这个 h 的 时候,是不是我们用平行四边的面积去除以 d 啊,对不对?那现在还是一样,我们要用平行四边形的面积去除以 d, 但是呢,我们这个平行四边形在这里啊,我们只告诉我们是三角形面积,对不对?所以你要利用三角形面积怎么去求出这个高呢?我是不是 三角形的面积先乘以二呢?是不是?所以这个平行四边形我们转化为两倍的三角形的面积啊,再除以底就行了,那你看两倍三角形面积是不是长这样子, 哎,这个乘以二是不是就变成了一个平行四边形啊?所以啊,我们求高,先将三角形的面积乘以二,转化成平行四边形, 然后利用平行四边形的面积去除以底,就出现高了。那么同样的,如果现在三角形让你去求这个底,先告诉你这个高和面积求底怎么求?很简单,你把这个三角形先转化为平行四边形,那就是两倍的三角形的面积去除以高 就搞定了,所以这简单吗?你看我们这一块很多同学,这个在到就是,这是我们的一个 公式的逆推啊,那么这公式我们怎么来?刚刚是不是说了,将三角形转化为平行四边形的计算对不对?所以都是通过这一个来实现的, 对吧?用面积平行四边的面积去除一条底,就出现一条高,用平行四边形的面积去除一高就出来底了啊。所以我们要将三角形和平行四边形的这个两倍的关系利用起来啊,那么我们接下来来探讨梯形的面积。 首先梯形啊,这条叫做上底,这条叫下底,上底用 a 来表示,下底用 b 来表示。那么这里我先说一下,上底和下底不是指的是位置关系,上底指的是梯形,那条比较短的叫做上底,那么比较长的呢,叫做下底,上底和下底是互相平行的,那这两条叫做腰。 那我们在实践探索的过程中,我们会发现三角形和梯形一样啊,那么只要你画出两个一模一样的梯形,就可以组合成一个平行四边形,那怎么组合的呢?它这样子的, 这个就组合好了,那你看这个上底就跑到下面来了,我们是把它倒立组合在一起啊,对不对? ok, 这个就是一 啊。那么现在变成平行四边形了之后,我们依旧通过平行四边的面积将梯形的面积推倒出来。那怎么推倒呢?很简单,我们刚刚说了,这个平行四边形的面积是不是等于底层高啊?对不对?所以这个面积将就底层高,我们把高画一下, 这是 h, 那 底现在是多少?平行四边形的底就是现在是 a 加 b, 这条是不是平行四边形的底啊?对不对?那底层高高是几高?是 h 是 不高就是这条 h 啊,我们会发现平行四边形的高跟梯形的高是一样的。 那我现在要算梯形是平行四边形的面积除以二,它就是梯形了,所以底层高除以二就是梯形的面积 是不很简单。好,那么接下来这个最最难的一个点就出来了,现在平行四边形的面积能够推导出梯形的面积,那请问如果题目中告诉我梯形的面积和上底下底怎么去求高, 那也就是说这个 h 怎么去求?那刚刚三角形听明白的同学肯定现在这个 h 迎刃而解, 很简单啊,我们通过平行四边形的面积去除以底,这高不就出来了吗?那你看这个,我要求这个高怎么去除以底啊?我是不是把这个梯形 是不是先乘以二?也就是说把它一模一样的男神兄弟给他先拿出来对不对?所以告诉你这个的面积之后,那么面积乘以二是不是就恢复成平行四边形面积了?平行四边形的面积告诉你了,怎么去求高,你去除以底哦,底是不是 a 加 b 对 不对? 所以这里还是一样的跟三角形,先把它的这个梯形的面积扩大两倍啊,扩大为原来的两倍,那么它现在就变成平行四边形的面积,对不对?这时候去除以底,底是 a 加 b 了, 好,这个是我们这一单元的比较难的一个公式了啊。那么接下来还有两个相对来说也是比较难的一个公式,也是在梯形里面的,如果现在告诉你梯形的面积,告诉你梯形的高,那么也告诉你上底怎么去求,下底呢?也就说这个 b 怎么求呢? 一样的,你先把它恢复成什么东西?平行四边形,那么我要求这条 b 是 多少?我只要用平行四边形的面积去除以高, 就算出这一条底了,对不对?然后用整条底去减去其中的一部分 a, 是 不是算出 b 了,对不对?所以这里还是一样用两倍的梯形面积 来,我用图简单画一下啊,比如说这是一个题型,现在呢?告诉你高 h 了,那现在这个 a 也告诉你了,现在求这条 b 怎么去求?先将这个题型 乘以二,变成平行四边形的面积,对不对?然后我们利用平行四边的面积去除异这个 h, 算出这一整条 底,那这整条底出来之后呢?我减去这条上底 a, 是 不是这条下底 b 就 出来了?这样子讲能听懂吧?所以它 b 就 等于两倍的面积 去除以高,算出上底加下底的和,也就是说平行四边形的这条底,然后我们减去其中的这一部分,也就是说减去上底 就出来了。所以这里记的方法很简单,我们求下底,我们用两倍的梯形的面积 去除以高,算出所谓的平行四边形的底,也就是说梯形的上底减下底的和,那你要求下底就减上底,那你如果求上底呢?那就是两倍的梯形面积去除以高, 算出所谓的平行四边形的底,然后你求上底,我就减下底。这时这里十个公式都出来了,分别是平行四边形有一二三,三角形有一二三, 题型是一二三四,而题型往往这个这一块啊,很多同学记忆的时候非常痛苦,那真的很难吗?不难,你要 一定要学数学啊,一定要带着理解去学的,你不能去死记硬背的啊,死记硬背背完了之后,你可能还是不会运用的,所以很多同学学数学实际上是很轻松的, 课堂听懂理解了,课后都不用去背,那么题目再落实一下,我们这一块内容就搞定了。 至此,我们这所有的公式一共十个,全部都搞定了。那哪十个呢?平均四边形三个,三角形三个,梯形一二三四四个,一共十个,对不对?特别是三角形的啊,反过来求底和高,或者梯形反过来去求 底和高,都是一大难点,特别是梯形啊,有上底和下底,对吧?公式相当复,相对来说复杂。那么有同学在那里 背的时候,只会什么 h 等于二 s 去除以 a 加 b 的 和他,甚至连 a b, h、 s 是 什么都不知道, 这种读书是很可悲的,而且很痛苦,你背完了有什么用呢?有同学 a、 b、 h、 s 连表示的意思都不知道,那你背这个东西的意义何在?你会运用吗? 所以学数学一定要用理科的思维去学,不要死记硬背啊,死记硬背,学数学很痛苦的,特别是这里这么多公式的情况下,根本就死记硬背,背不了,过两天就忘啊,一定要理解他们是怎么来的。
 04:55查看AI文稿AI文稿
04:55查看AI文稿AI文稿阿道爷爷有一个梯形的花圃,这个花圃的面积是多少呢? 梯形的面积计算公式我们还不知道,那我们把梯形转化成学过的图形,来推导梯形的面积计算公式。 我们可以运用拼摆法,把两个完全相同的梯形拼成一个平行四边形,那梯形的面积就等于拼成的平行四边形面积的一半。 拼成的平行四边形的底等于梯形的上底与下底的和高,等于梯形的高。 因为平行四边形的面积等于底乘高,所以每个梯形的面积等于上底加下底的和乘高除以二。这样我们就推导出梯形的面积计算公式了。 还可以怎么推导呢?可以运用分割法把梯形分割成学过的图形,如画出梯形的一条对角线,则可以得到两个三角形,那梯形的面积就等于两个三角形的面积之和。 我们过这个点做出梯形的高,这条高也是三角形一这条边上的高,而三角形二这条边上的高与梯形的高相等,所以两个三角形的高相等,都等于梯形的高,那我们都用高来表示。 三角形一的面积等于梯形的下底乘高除以二。三角形二的面积等于梯形的上底乘高除以二, 梯形的面积等于这两部分相加,也就等于梯形的上底加梯形的下底的和乘高除以二。 当然还有很多推导梯形面积计算公式的方法,同学们课外可以自己去研究一下哦。 如果用 s 表示梯形的面积,用 a 表示梯形的上底, b 表示梯形的下底, h 表示梯形的高, 那梯形的面积计算公式用字母表示为 s 等于 a 加 b 的 和乘 h 除以二。 知道了梯形面积计算公式,我们就能求出阿道爷爷花圃的面积了。 花圃的面积等于上底加下底的和乘高除以二等于五,加十的和乘五除以二等于十五乘五除以二等于三十七点五平方米。 所以这个花圃的面积是三十七点五平方米。我们再来做一道题,一个梯形的上底是四点二厘米,高是四点六厘米,面积是二十三平方厘米。梯形的下底长多少厘米? 我们可以直接运用梯形的面积计算公式列方程解析。设梯形的下底长 x 厘米,根据题意可列出方程,四点二加 x 的 和乘四点六除以二等于二十三。 方程两边同时乘二,得四点二加 x 的 和乘四点六等于四十六。方程两边同时除以四点六,得四点二加 x 等于十。 方程两边同时减四点二,解得 x 等于五点八。答,梯形的下底长五点八厘米。 其实也可以根据 s 等于 a 加 b 的 和乘 h 除以二,推导出 b 等于二, s 除以 h 减 a, b 等于二十三,乘二除以四点六,减四点二 等于四十六除以四点六减四点二等于十减四点二等于五点八厘米,同样能算出梯形的下底长五点八厘米。 最后总结一下,梯形的面积等于上底加下底的和乘高除以二,用字母表示为 s 等于 a 加 b 的 和乘 h 除以二。 如果已知梯形的面积上底、下底和高中的任意三个量,我们可以通过列方程求出另一个量,也可以用算数法求出另外一个量。怎么样,你都学会了吗?
 01:16查看AI文稿AI文稿
01:16查看AI文稿AI文稿这种题型一定会考到,出错率特别高,根据给出的已知信息,让我们去求这个多边形的面积。今天教你一个小技巧,我们可以用添补法, 我们把上面缺失的这一部分给他添补完整,他就变成了一个直角三角形。在直角三角形中,这个角是四十五度,那上面这个角也是四十五度。添补上了以后,他就构成了一个等腰的直角三角形,这条边是八厘米,那同样这条边他也是八厘米。 我们先求出这个大三角形的面积,那就是八乘八,再去除以二,然后再来求这个小三角形的面积。这个角是直角,那这个角是四十五度,他的角和他的度数相同,也是四十五度,那这条边是二厘米,同样这条边也是二厘米, 它的面积呢就是二乘二,再去除以二。最后我们就用这个大三角形的面积减去小三角洲形的面积,得到的就是这个多边形的面积,等于三十平方里,这就是求多边形面积必会的割补法,还有平移旋转法、 龙翕法等等。这里把五年级所有常考的关于求面积的易错题型都给规范总结好了,这里的每一道题扫码都可以看视频讲解,后面还有小学几何必会的八大模型,让孩子把这些方法都学会了,期末怎么考都不怕了,赶紧准备吧!
133四五年级(知识课堂)














