阴影面积减速带的公式
这种求阴影面积的题肯定是很多同学的噩梦,并且你也可能看过很多的动画拆解,但是一到考试的时候你就全都忘了。 那这种图形的题其实就分为有重叠和没有重叠两个类型。什么叫有重叠?你看我上面的这个图啊, 它就是由两个半圆重叠在一起,构成了中间的这个阴影部分。好,那你现在呢?就把图中你看到的所有图形标上序号。好,我标的是一号、二号、三号、四号和五号。 现在你能认识的图形有两个半圆和一个三角形。好,第一个半圆是由一号、二号和三号组成的,另一个半圆是由三号、四号和五号组成的,三角形是二号、三号和五号。 那么我们再来找一下阴影部分,阴影部分是由一号和三号的,另一个半圆当中有四号,那我们就把这两个半圆加在一起。 但是现在我们多了二号、三号和五号,那我就得把这个二号、三号和五号减掉。哎,那这个时候你会发现二号、三号和五号是不是刚好是刚才的三角形? 那这道题的结果就出来了,两个半圆减去三角形就可以了。那咱们再找一个这种题啊,再找一个难一点。好,你看这个图, 这个图看着中间好像有一朵小花来,同样他也是有重叠的,你能发现他其实中间是有四个半圆吧,并且阴影部分也有重叠。好,还是老套路,我们先给他们标上序号,一二三四五六七八。 那么我的第一个半圆就是一号、三号、五号,第二个半圆是二号、七号、四号,最后一个半圆是三号、八号、四号。 好,那你还能看到一个正方形,那其实正方形是不是就是一二三四、五六七八?那现在阴影部分是一二三四。哎,我发现第一个半圆有一号,第二个半圆有二号,第三个半圆有四号,最后一个半圆有三号。 好,那现在我是不是可以把这四个半圆加在一起?加在一起之后我发现多余的部分正好是序号,一二三四五六七八, 一二三四、五六七八,是不是就是正方形的这个整体?所以这个图求阴影面积,其实就是四个半圆加在一起,或者你说两个圆加在一起减去正方形就可以了。
粉丝120获赞902
相关视频
 04:26查看AI文稿AI文稿
04:26查看AI文稿AI文稿上一期视频啊,王老师来讲了求涂色部分的周长问题,那有的同学在评论区里面告诉王老师,你能不能求这些阴影部分的面积呢?那今天王老师这这期视频呢,就来讲一讲如何来求阴影部分的面积题。 那首先我们来看这个图形,各位同学们来观察这个图形,让我们求阴影部分的面积,那阴影部分包含两部分,是这一部分和这一部分。同学们发现 这呢是一个以直径为二十厘米的这样一个半圆,那么同时我又以二十厘米为半径的画了这样一个扇形,我在这里我只需要做一道小辅助线。那么同学们来观察, 因为这个角呢,它是一个直角,那这个三角形呢?是一个等腰直角三角形,而且这两条呢都相当于是一条半径。我现在连接这两个点,各位啊,我们来观察 连接这两个点以后,大家看这是这也是两圆的半径,对不对啊?这两个三角形什么关系啊?面积是完全相同的, 因为这是一个半圆,所以他俩相同,那他俩面积是不是也相同?那现在我就把他给他怎么样移到这里来,因为他俩的面积相等,那现在我把他给移过来, 移过来以后,那现在我把原来的这部分怎么样给它擦掉,那这样我就 把阴影部分的面积怎么样给它放到了一起。那要求现在阴影部分的面积,我是不是可以用这个扇形的面积减去这里的这个直角三角形的面积。 那这个扇形的面积,它是占圆面积的什么八分之一啊?因为这个是圆心角呢,是四十五度啊,我们这个圆的面积是派二的平方,二呢是二十,二十的平方乘 三百六十度分之四十五度,这是圆面积的八分之一,为这个扇形的面积,然后再减去这个直角三角形的面积,那这个直角三角形的底是二十,那高是不是二十的一半,那就是二十乘 二十除以二啊?底乘高,然后再除以二。来,我们来计算一下啊,二十的平方是四百四百乘八分之一是五十,五十,派是一百五十七减 二十,乘十是二百二百,除以二是一百,一百五十七减一百,那结果是五十七 平方厘米,简不简单呢?易不易懂啊?来再来看第二个,那第二个这个阴影部分面积,其实就是可以用长方形的面积怎么减去这个半圆的面积啊? 这是一种方法,那其实我们还可以,各位,我再拿一个和他怎么样面积相同的这个图形,大家看啊,我现在我再拿一个面积相同的这个图形,各位啊, 那么我们可以把它放在了,是不是就相当于是一个方中圆的问题,那既然是方中圆的问题,我用正方形的面积减去圆的面积,再除以二,那不就是 这个阴影部分面积吗?其实方中圆的面积有个公式还记不记得,那就是正方形的这个面积减去圆的面积,我们知道是是不是零点八六 r 的 平方,因为是零点八六 r 的 平方的一半,所以那就直接用零点八六 r 的 平方,是不是除以二, 那就等于零点八六除以二,是不是零点四三啊?那就是零点四三,那就是乘四 乘四的平方。四的平方是多少?是十六来零点四三乘十六是多少呢?零点四三乘十六来三六十八进一四六二四加一是二十五,一三得三,一四得四八八六。 所以最终求出啊,这个阴影部分的面积呢?是六点八八平方厘米。那对王老师所讲的黑板上的这种非常具有代表性的求涂色部分面积的题,学会了吗?关注我和老师赶紧收藏起来教娃吧!
387王老师爱叨叨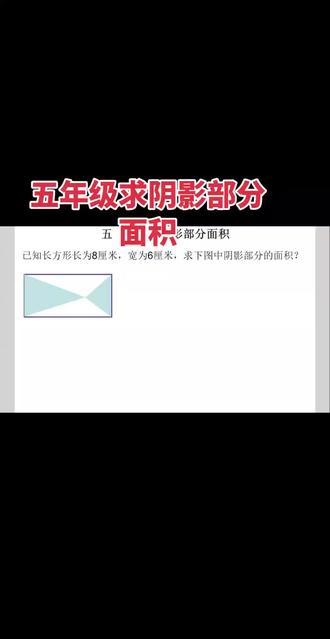 02:45查看AI文稿AI文稿
02:45查看AI文稿AI文稿今天给大家分享的是五年级上册求拎领部分的面积,已知长方形长为八厘米,宽为六厘米,求下图中拎领部分的面积。 这里用到的知识点呢,是我们三角形的面积公式也是底乘以高除以二,而图中求的拎领部分的面积呢,刚好是两个三角形面积相加, 并且从图中我们不难得出,三角形的底边呢为六,刚好是我们长方形的宽,那 它的高是多少呢?这个时候我们来做一条辅助线,就不难发现,这个三角形的高 h 一 和这个三角形的高 h 二呢,它下加起来刚好是我们长方形的长,也就是 h 一 加上 h 二呢,等于八。 那三角形的面积公式是底乘以高除以二,所以我们这个三角形的面积公式呢,是六乘以 h 一 加上啊除以二,而这个三角形的面积呢,是等于这个六乘以 h 二除以二。我们 把它写出来之后,发现可以用到乘法结合率,也就等于三乘以括号 h 一 加上 h 二,而 h 一 加 h 二呢,可以等于八,进行等量替换,就算出我们厘米部分的面积呢,等于二十四平方厘米。 这个题型呢,也是我们平行四边形一半模型的经典题型。那一半模型呢,一般是用于选择题和填空题,可以直接给答案,但是在计算题中呢,一定要写过程,不然你是没有分的。那这里呢,也给大家总结了四种图形,这四种图形呢,也是可以用于 用平行四边形一半模型呢去直接解析的。那首先第一种呢,它是平行四边的对角线呢,把平行四边形分成两个三角形,而这两个三角形的面积相等,都等于平行四边形的面积的一半,这里呢是等底等高的原理。 那第二种图形呢,是两条对角线,把它分成了四个三角形,那我们上面这个三角形和下面这个三角形的和呢,刚好也是我们平行四边形密集的一半,同样的用到的是等底等高的原理, 那这里呢,第三个图形呢,是在平行四边形的一个顶点,一条边上顶点与下面这条边结合的一个三角形呢,他也是平行四边形的面积的一半,同样的用到了等底等高的原理,也就是这条边呢,和这条两条边相加呢,是相等的高相等嘛? 那同样的呢,我们这个顶点如果是动到了平行四边形的外面,在这边或者这边都是可以的,那它组成的三角形的面积呢,也等于平行四边形面积的一半,同样的用到的是等底等高的原理,你听明白了没?
50艳群老师 01:49
01:49 02:04
02:04













