凹凸二次函数列表
大家好,今天我们就来讲一下函数的凹凸性,实际上高中的时候已经学过一些函数的场景性者,比如说函数的单调性、 基友性、对称性、周期性,对吧?那今天我们讲下一个性质,凹凸性,非常重要的一个性质。那什么是函数的凹凸性呢?咱们先说一下这个统计版,这个教材是怎么说的啊?比如说在这个区间 i 上,这就是那个区间 i a b 之间吗?然后呢,认取两个数字, x 一和 x 二, 好,然后 x 一 x 二这个终点位置呢?那就是二分之二 x 一 x 二。显然,如果这个函数向下突的话,我们看红色这一段, a、 d, b 这一段,如果这个函数向下突的话,那么就会产生这样一个结果,对于任意的 x 一 x 二, 当然了,在曲江爱上,嗯,都会产生什么结果都有。二分之 x 一加 x 二,就是说中 终点横坐标重点所对应的这样一个函数值呢,它是小于二分之 fx 一加上 fx 二。注意,必须有这样一个任意性啊。那此时的话,我们就说这个函数呢,是凹函数,或者说是向下吐的,其实都是一回事啊, 那么为什么会这样呢?其实好说,你如果写上 x x 二,如果写上直线的话,你看这两个点,直线连着直线,那如果说在上边这样一个点 e 的位置在直线上啊,那 mn 中点是不就是点 e 啊?根据终点的公式,这个位置就变成等于了吧,小于号就是向下图的意思, 但是这个定义严谨吗?我想说的是同级版教材里头这个定义并不严谨,我非得找终点啊。如果一个函数他真的是向下图的话,我非得找 ab 的终点吗?难道你只能找中间这样一个点啊?我找四分之一点比他低行不行啊? 我判断他下图的时候,我找三分之一点可不可以?其实也可以的。所以说真正严格的数学分析里头的定义啊,是这么说的,设函数在区间 ab 内有定义,这个呢就是小 a, 这就是小 b。 看清楚了啊, 如果对于区间 ab 内的任何两个点, x x 二以及任何的两个,这个应该说是两个正数,而且这两个正数之和等于一,很有什么?很有这个这个呢?我知道很多同学看不懂,实际上呢,高中时候咱们学平面相量时候学过什么 定比分点定理吗?是不是根据平面限量的三点共享定理?而且啊,我们让这个蓝莓的一加上蓝莓的二等于多少等于一就可以了,此时肯定会有 om 项链,他等于多少等于蓝莓的一倍的 oa 项量, 再加上咱们的二倍的 ob 项链,然后你把项链的表示写成坐标的表示,就会有这样一个结果了。这大家看清楚 一定理解是怎么回事啊?其实也就是一个定理,难定理,他就完全代表什么?完全代表 ab 之间,或者说 x x 之间所有的点都是严格低于谁的?严格低于中间连线上这样的点的什么意思啊?这个就是 x 一,这个就是 x 二, 这个点呢?是 m 右边这个端点呢?写成 n 点,我们 m n 的话连了一条直线吧,实际上就是随便说,他说当这个 x 零随便取的时候,永远能够保证谁永远能够保证他下边对应的这样一个函数值,看向下图吧, 永远保证了 q 点是比 pgl 低的,所以就是向下突,理解了吧。那如果把中间这样一个小于号改成了什么?改成大于号,那就是向上突呗,就是一个意思。那既然有了这样一个定义之后的话,接下来我们就要说特殊的类型了,如果这个函数, 如果这个函数在开区间连续 b 区间, b 区间有二次倒数,有二阶倒数,那肯定有一阶倒数吧。 所以我马上就想到了什么科技种植定理,拉格朗尔种植经理,所以一会我们证明的时候,估计要用到微分种的定理了,一会再说啊。 有二阶导航数,那么什么意思啊?如果在 ab a 到 b 这样一个开圈内,二阶导函数是严格大于零的, 知道我刚才为什么说严格的大于零吗?他是这个意思,在 ab 任何这样一个字体内不能横为零。你如果说某一小段横为零的话,他这个就没有凹凸性了,是横直走的,应该理解我的意思吧,就是中间这一段,这一小段是直线了,这理解就行。 那么第二点,如果说二阶倒函数严格大于零的话,那就是向上图的,而且不存在横为零的情况。二阶导函数千万不要横为零,因为如果二阶导函数在某一小段横为零了, 那就意味着在这一小段上一届导航数,其实也就是速度。怎么样?速度呢?很为一个定制,我们不可能要求速度是一个很很为定制的情况。为什么 看向下凸这速度原来是个复数吧,一直走一直走,一直走啊,速度越来越大,速度一直得变大啊。这个呢,实际叫什么?这个就叫向下凸的情况。 那现在我们就想证明了,怎么证明啊?刚才说过了,人家这个函数在 b 区间连续在开一间课道,你为什么不想一下?什么终止定理,拉个脑的终止定理吗?接下来我就要写这个证明过程了啊,图我放小一点啊,这样来标,先标这个 x 一,再标这个 x 二,这个 x 一和 x 二是任意取的, 然后呢,这个 x 零肯定在 x 一和 x 二之间,根据刚才我讲的这个定比不点定理,我们这个 x 零完全可以怎么取啊?我们这个 x 零完全可以取成这个栏目的一啊, x 一,再加上栏目的二 x 二,当然咱们的一,咱们的二的话都是两个正数啊,都是正数,并且呢,咱们的一,咱们的二加起来必须等于一,对吧,这样就保证了 x 零肯定是中间任何一个位置都可以包含进去了。 那么再接下来怎么样呢?当然了,一开始我们取这个 x 一和 x 二的时候,实际上肯定是在这个 ab 之间任意去取的,保证这个任意性,并且我们不妨令这个 x 一比 x 二小吧。那最终我们的目的实际上非常简单,经过中间的一番论证,这个论证过程肯定是要用拉格朗式终结定义,我一会再写, 最后证明出来什么结果,那肯定是定义里头我们挣哪个呀?不妨我们就来证明这个括号一吧,只要括号一证明完了,括号二肯定会了,那最终我们想证明的就是谁?就是这个 f 啊,兰博大一 x 一,然后再加上兰博大二 x 二,他是小于谁的?他因为在下方,我们是向下图的, 所以是小于小于咱们的一 f 一,咱们的二乘 f 二,就这样一个道理,这就是我们我们的目的。那具体怎么操作?拉格朗是中指定理,走起来。为什么?一开始我在读这个定义,读这样一个定理的时候说过了, 在哪?在 b 局间连续开局间课道肯定要想一下。微分钟定理,具体来说就是拉格朗式中定力,我写了啊,首先在哪啊? 在 x 一到 x 零中间,那肯定满足拉格朗式中指定理了吧?那这个 x 零减 x 一的话,我们这个 x 零怎么写?你把画圈部分带入啊,最终的话就写成了什么结果,最终的话,我们就写出来了这样一个结果,人们的二倍的 f 片,哦, 在一,然后这个括号里头是 x 二减 x 一,那行,并且在哪一段呢?实际上在 x 零到 x 二之间也是满足, 在 x 零到 x 二之间,他也满足这个微分钟定理。拉格朗式充值定理我们就直接写啊,所以说 f x 二减去 f x 零,他就是等于 f 片,这个时候我们因为这个值不一样啊,我们就要改成 f 片科赛二了, x 二减 x 零, 同样的,我们不要出现 x 零嘛,我们最终只出现 x x 二,所以就是化球部分往这一带啊,最后就只含有这个蓝莓的一了,么的二,还有这个 x x 二了,最后提出来的是蓝莓的一倍的 f 片,哦,这个里头是科赛二啊, x 二加 x 一。好啊,现在我们观察一下这个圈一圈二就行了, 看最后这个结果吗?最后的话,他这个系数是多少? number 二啊,这个圈儿这个狮子呢? number 一,那行啊,所以我们在处理这个,嗯,圈儿一圈儿的时候,最终目的也很简单嘛。最终根据定义,我们 这个圈二要乘个多少?肯定是要乘个栏目的二嘛,乘个栏目的二,嗯,然后呢?这个圈一啊,区二一的话,我们就不妨乘一个数字,乘一个数字栏目的一,这样的话,区二一就要圈二,左边和左边相减,然后右边和右边相减,别忘了乘上对应的系数栏目的一了。么的二啊, 最终出来的结果非常的有趣,我就直接写了啊。最后经过处理的话,就出现这样一个结果了,左边的话,你看是不是 lam 的一,然后乘外一 m 的二,乘外二减去 fx 零,这个 x 零不就是画圈这个整体吗?一会我们再变,不着急,关键是要看右边这个部分究竟是大于零还是小于零,还是等于零,对吧。先看了 第一部分,两个正数相乘正数吧。第二部分,大的数字 x 二减小的注,数字 x 一正数吧。有人到了第三个圈的部分,说,不会了,老师,这个 f 撇可在二和 f 撇可在一。我确实不知道哪个大 哪个小,这个还不好判断啊。请你告诉我,既然我们证明的是区二一,这个二阶导函数是不是严格大于零?二阶导函数大于零,不就意味着这个 f 片一阶导函数是单调递增吗?你这个科赛二比科赛一大,所以对应的函数值肯定是大的减小的,大的减小的,最终经过单调性的讨论,他也是个正数, 三个正数相乘啊,同学们经过了一番讨论,当然这个讨论需要你写出来啊,考试时候我们是大于零的,大于零最终不就得出来这样一个结果吗?这个 x 零,我们需要还原成什么形式,写成画圈的这样一个形式带进来啊,我们换一下吧,这个 x 零,注意啊,变化成那么的一 x 一, number x 二,所以说直接下结论,往哪啊?往下图呗,他就是一个向下图的函数,也就证明完了。接下来呢,就是对于这个拐点的定义,拐点的话也好说,看 这个位置。哦,原来呢,在这一段上,他是向上涂的,然后到 a 点呢,到 c 点这个位置啊,就变成什么了?就变成向下涂了,一个向上涂,一个向下涂,那 a 点这个坐标点的话,他 这个题目中说的是 m 点,我们就写上 m 点吧,那 m 点 x 听外联就成,为什么?就成为这个曲线的拐点,所以直观上来说的话,拐点就是什么?就是凹凸性发生改变的点。那严格的定义是怎么说呢?是这样说的啊,假设 m 点呢,是这个函数图像上的一个点,一个坐标点, 如果这个曲线经过 m 零的时候,凹凸性发生了改变, m 量左边是上图,右边变成下图,或者说左边下图,右边上图,反正是凹凸性发生了改变,那此时我们称这个坐标点就是 y, 等于 fx 这样一个曲线的拐点。现在应该懂拐点的意思了吧。后边补充一条啊,如 如果说 m 点是这个函数的拐点,那么它存在的必要条件,必要条件就是箭头指向谁,指向指向条件的意思啊,有结论,指向条件就是这个二阶倒函数等于零,或者说什么,或者说这个二阶倒还是不存在的, 现在我们对比一下,也说一下这个注点啊,注点的话是一级导航,是为零的点,也就是说这个函数呢,正好停起来速度正好停下来的点,懂了吧?那么急支点的话一定是注点,注点的话就不一定是急支点了,我们看啊,前头的话好说,为什么注点不一定是急支点呢? y 等于 x 三次方吗?大家可以观察一下这个函数图像,你也可以求导确定一下,在零到正无穷的时候呢?单调递增,在这个复活圈到零,他也也是这个单调递增, y 等于 x 三次方,但是有没有注点?有,因为他的一阶导航 数什么时候当 x 等于零的时候,原来 x 等于零就是他的这样一个注点一定要区别,注点和拐点区别还是很大的,注点是横坐标的直吧,拐点是某一个函数图像上的坐标点。 另外的话,这个注点和旗帜点它定义也不一样,一个是一阶段还是等于零定义的,另外一个是二阶段,还是数来定义的,所以呢,一定要注意区别了。那接下来咱们做两道题吧,第一道题, 第一道题的话求倒背第一届倒数啊,当然所有的函数问题我们应该先写什么?你应该先判断一下这个定义吗?定义是人也是数,这个就不多说了, 那接下来看一下谁呢?看一下这个一阶倒函数吧。一阶倒函数我们求一下啊,马上就求出来了,他是等于负二 x 一负 x 方的这二阶导函数呢,也好求。嗯,二阶导函数求完之, 明显发现这个画圈部分是正数,二也是个正数,所以呢,二阶段还是个正步,取决于什么?取决于画圈的中间这个括号。我们令他等于零呗, 对吧?另,这个外片片等于零,马上就得到谁了?马上就得到两个值,其中一个呢,是负二分值,根号二,另外一个呢?是啊,二分值,根号二。其实呢,这两个值我想说的,他不叫拐点,他叫什么?他叫拐点对应的行,坐标。人家拐点是个坐标点的啊。 接下来分呗。你想啊,整个实属范围内被这两个分成了几段?分成了三段。那为什么出现了这样一个表格?马上你就知道了。我们先看啊, 先分什么?负无穷到负二分之根号二,这肯定得写一下,对吧?然后负二分之根二单独写一下,负二分之根二到正二分之根号二拎出来,还有一个正二分之根号二单 都写一下,最后一段的话,肯定是二分之根号到正无穷了。这样的话,所有是书房内的电影院,这个数字都讨论全了。 那么接下来判断政府好说吗?中间是负的,两边是正的呗。好说,那再接下来呢?然后这个位置是,而且倒还是为零。 那继续来,我们现在研究的是什么?研究的是原来这个函数,他的凹凸性和拐点吗?好哦,他是大于两,所以是向下图,或者你想凹函数也行啊,每一个他这个很多高等数学教材,他的说法不一样啊。 然后,嗯,如果为负的话,就是上图,然后下图啊,就这么回事啊,不多说了,那么零呢?零的话,千万不要以为拐点是什么点,拐点可不是横坐标,拐点是个坐标点,我们写全了负二分之根号二带入,纵坐标的话是一负二分之一,这个就是一个拐点。 好,我们写上其中一个,另外一个还要拐点吧,我们把谁带入啊?把这个二分之跟二二带入,然后呢? 最后上完中指标还是一,那因为他是个偶函数吗?大家能看出来也是这样一个结果,他也是一个拐点,两个拐点,应该清楚了吧?那 最后下结论的时候,大家只需要说啊,在这样一个区间上,他是向下凸的一个函数,在中间这样一个区间上是向上凸的一个函数,然后在这个区间上呢,又是向下凸的函数,然后再把这两个拐点坐标写上就行了。 下一个题道理一样,只是说解题是不一样,所以呢,我就直接写结果了,二阶导航数跟零比较,就可以确定这个凹凸性了,对吧? 那接下来我们就求出来两个值,其中一个是零,另外一个不就是三分之二了吗?是不是?那还是画表格吗?零三分之二 x 复无穷到零,写上,把零单独拎一下,零到三分之二 是不是也写一下啊?三分之二单独拎出来是吧?然后最后的话是三分之二到正无穷。讨论全了,接下来写这个二阶导函数的值,或者说正负,嗯,显然他是正的吧, 哎,中间是负的吧,他又是正的。然后呢,在零和三分之二这两个点处呢?二级头还是等于零?那再接下来我们就直接写原函数的凹度性就行了啊,然后三分之二几你带入原函数中,三分之二算出来是二分二十七分之十一。好了,两个拐点卸全了。最后要写一下答案,从上所述啊。好, 好了,在服务群到零上是向下突的,当然三分之二到中国群也是向下突的。在哪?在零到三分之二中间,这个方案呢?是向上突的。那么这节课你学会函数的凹凸性了吧?分享课堂知识,感受数学之美或上班老师,下节课再见。
粉丝82.5万获赞397.1万
相关视频
 03:11查看AI文稿AI文稿
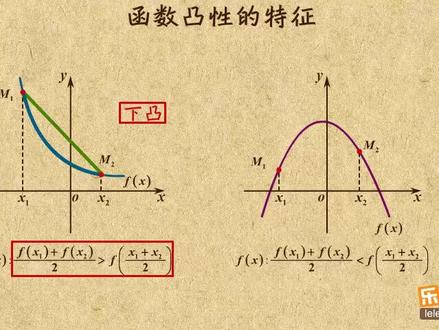
03:11查看AI文稿AI文稿这个视频我来给你讲讲函数凸性的特征。简单的分,函数凸性有两种长,这样叫向下凸,而这样是向上凸,他俩有啥不同呢? 先看向下图的函数,在图像上任意去两个点, m 一和 m 二,连接 m 一 m 二,发现没?函数 fx 在区间 x 一到 x 二上的图像总是在线段 m 一 m 二的下方, 而向上图的函数同样取点连线函数 fx 在区间 x 一到 x 二上的图像就总是在线段 m 一 m 二的上方,这就是函数凸现的几何特征。接下来我给你讲讲他的代数特征。 先看向下图的取线段 m 一 m 二的重点,哎,那他的横坐标就是 x 一跟 x 二的平均数二分之 x 一加 x 动作标就是 fx 一和 fx 二的平均数,也就是二分之 fx 一加 fx 二。 而图像上这个点 b, 他的横坐标是二分之 x 一加 x 二,那动作标就是 f 二分之 x 一加 x 二, a 在上, b 在下,所以 a 的动作标就大于 b 的动作标。这就是下图函数的代数特征。 只要函数图像向下图,在定义域内都有二分之 f x 一加 f x 二大于 f 二分之 x 一加 x 二。 反过来,如果以至函数 fx 取定义域内的任意时数 x 一和 x 二,函数解析式都满足这个不等式,那图像就一定是向下度的。 用类似的方法能够证明上图函数的特征跟他恰好相反,你只要把大于号换成小于号就成。反过来, 如果知道函数 fx 取丁域内的任意时数 x 一和 x 二,函数解析式都满足这个不等式,那图像就一定是向上图的。 前面讲的这两点,对于所有的图像为弧形的函数都是成立的,比如这两面函数在第一向前, x 的三分之四四方的图像长这样,是向下吐的,那对于任意的正式数 x 一和 x 二就都有二分之 f x 一加 f, x 二大于 f 二分之 x 一加 x 二。 而 x 的三分之二四方的图像长这样,是向上图的,那对于任意正式说 x 一跟 x 二就都有二分之 fx 一加 fx 二。小于 f 二分之 x 一加 x 二。 再比如指数函数二的 x 四方图向下图,那对于任意时数, x 一和 x 二都有二分之 x 一加 fx 二大于 f 二分之 x 一加 x 二。而对数函数 log 二 x 图像长这样向上图,那对于任意正式说, x 一和 x 二都有二分之 fx 一加 fx 二。小于 f 二分之 x 一加 x 二。 好了,讲了这么多,总结下吧。这个视频我主要给你讲了函数凸型的特征,对于图像为弧形的函数都有落图像向下图,则二分之 fx 一加 fx 二大于 f 二分之 x 一加 xr。 若图像向上图,则二分之 fx 一加 fx 二。小于 f 二分之 x 一加 x 二。怎么样,明白了吗?明白了就赶紧刷题去吧!
140在线学习高中部 01:25
01:25
















